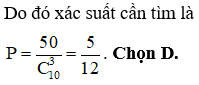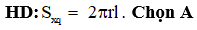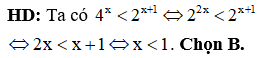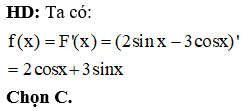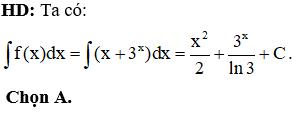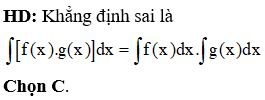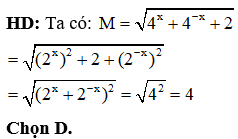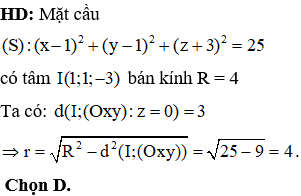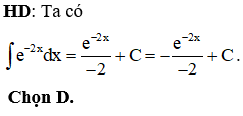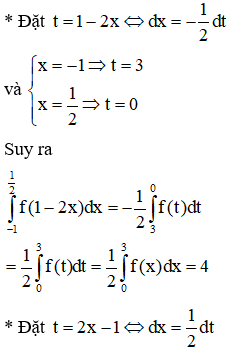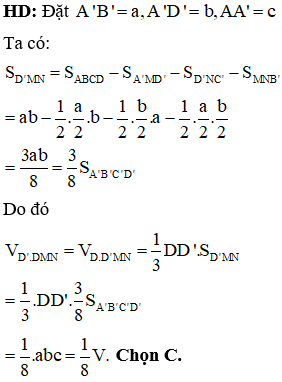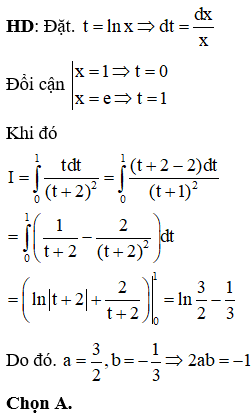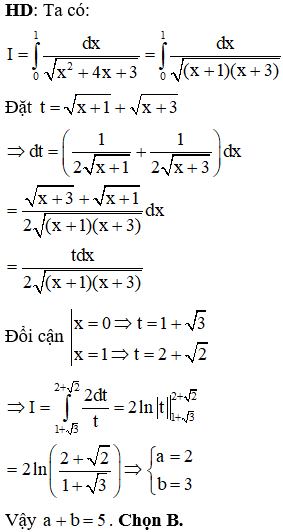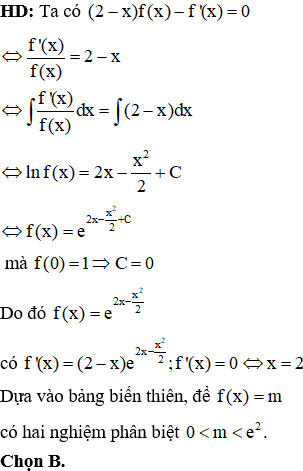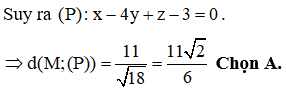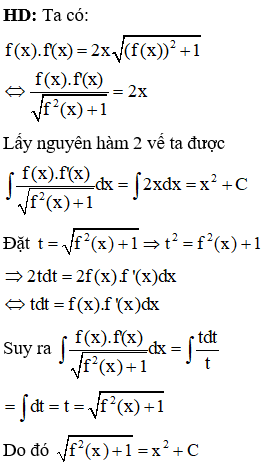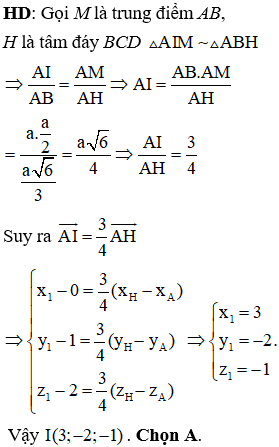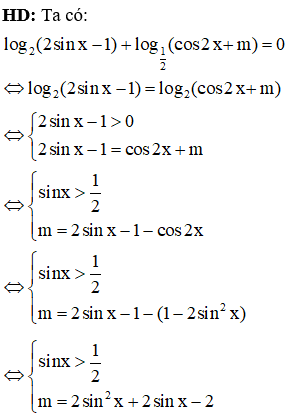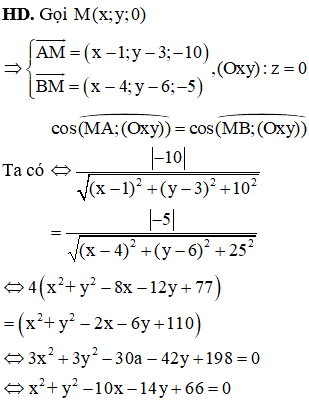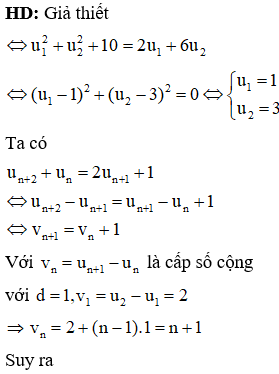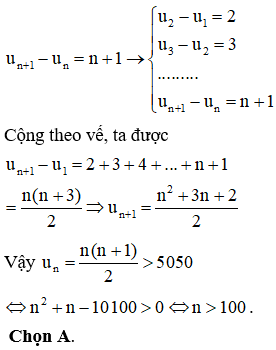30 đề thi thử thpt năm 2020 môn Toán cực hay có lời giải chi tiết
30 đề thi thử thpt năm 2020 môn Toán cực hay có lời giải chi tiết (đề số 21)
-
20068 lượt thi
-
50 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 4:
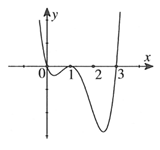
Đồ thị hàm số nào trong các hàm số được cho dưới đây không có tiệm cận ngang?
Chọn C.
Câu 14:
Cho hình nón có thiết diện qua trục là tam giác đều cạnh bằng 2α. Tính thể tích của hình nón
Câu 16:
Cho hình chóp S.ABC có SB vuông góc với mặt phẳng ABC, đáy ABC là tam giác vuông cân đỉnh B cạnh huyền , mặt bên (SAC) hợp với đáy một góc Tính thể tích khối chóp S.ABC.
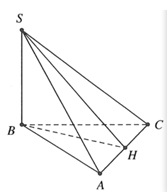

Chọn A
Câu 24:
Cho hình phẳng (H) giới hạn bởi các đường , . Tính thể tích của khối tròn xoay tạo thành khi quay hình (H) quanh trục Ox.
HD: Thể tích của khối tròn xoay tạo thành khi quay hình (H) quanh trục Ox là:
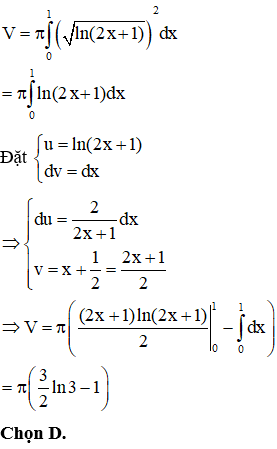
Câu 28:
Cho hàm số có đồ thị (C). Tìm m để đồ thị (C) có hai điểm cực trị A, B và đường thẳng AB vuông góc với đường thẳng

Phương trình đường thẳng đi qua 2 điểm cực trị là
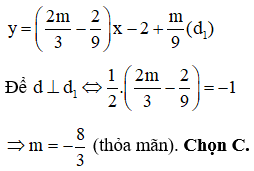
Câu 31:
Một người gửi 100 triệu đồng vào một ngân hàng với lãi suất 6%/năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào gốc để tính lãi cho năm tiếp theo. Hỏi sau ít nhất bao nhiêu năm người đó nhận được số tiền nhiều hơn 300 triệu đồng bao gồm cả gốc và lãi? Giả định trong suốt thời gian gửi, lãi suất không đổi và người đó không rút tiền ra.
HD: Số tiền cả gốc lẫn lãi của người đó sau n năm là: T = 100(1 + 6%)n
Để số tiền nhiều hơn 300 triệu thì:

Vậy sau ít nhất 19 năm người đó nhận được số tiền nhiều hơn 300 triệu. Chọn A.
Câu 33:
Một hộp đựng 11 tấm thẻ được đánh số từ 1 đến 11. Chọn ngẫu nhiên 4 tấm thẻ từ hộp. Gọi P là xác suất để tổng số ghi trên 4 tấm thẻ ấy là một số lẻ. Khi đó P bằng:
HD: Số phần tử của không gian mẫu là:
Gọi A là biến cố: “Tổng số ghi trên 4 tấm thẻ ấy là một số lẻ”
Khi đó số tấm lẻ được chọn là số lẻ.
Trong 11 số từ 1 đến 11 có 6 số lẻ và 5 số chẵn.

Câu 34:
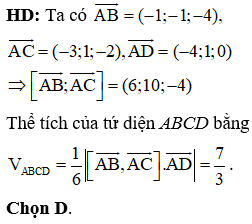
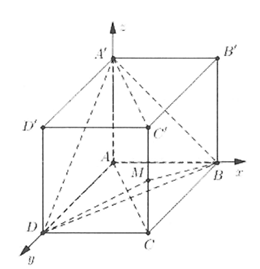
Trong không gian Oxyz, biết mặt phẳng (P) đi qua điểm M(1;4;9) và cắt các tia dương Ox, Oy, Oz lần lượt tại ba điểm A, B, C khác gốc tọa độ O sao cho OA +OB+OC đạt giá trị nhỏ nhất. Khi đó chọn khẳng định đúng
HD: Gọi tọa độ ba điểm A, B, C lần lượt là


Vậy độ dài ba cạnh OA, OB, OC lần lượt theo thứ tự lập thành cấp số cộng. Chọn C.
Câu 36:
Tìm m để đồ thị hàm số có ba điểm cực trị A; B; C sao cho OA = BC , trong đó O là gốc tọa độ; A là điểm cực đại, B và C là hai điểm cực tiểu của đồ thị hàm số.
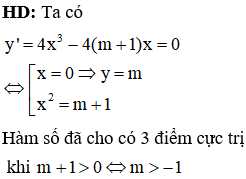
Khi đó điểm cực đại của đồ thị hàm số là A(0;m) và tọa độ 2 điểm cực tiểu là

Câu 40:
Cho lăng trụ đứng . Gọi I là trung điểm của CC'. Tính cosin của góc tạo bởi hai mặt (ABC) và (AB'I)
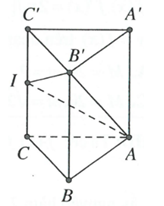
HD: Dễ thấy ABC là hình chiếu vuông góc của AB’I trên (ABC)
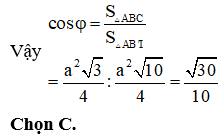
Câu 46:
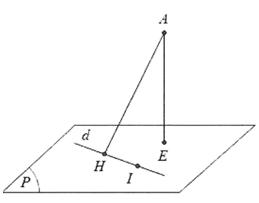
Cho hình trụ có chiều cao bằng bán kính đáy và bằng 4 cm. Điểm A nằm trên đường tròn đáy tâm O, điểm B nằm trên đường tròn đáy tâm O’ của hình trụ. Biết khoảng cách giữa 2 đường thẳng OO’ và AB bằng cm. Khi đó khoảng cách giữa O’A và OB bằng:
HD: Hình vẽ tham khảo
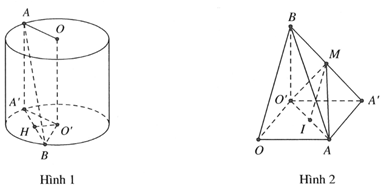


Chọn D
Câu 49:
Một đa giác lồi có 10 đỉnh. Chọn ngẫu nhiên ba đỉnh của đa giác và nối chúng lại với nhau ta được một tam giác. Tính xác suất để tam giác thu được có ba cạnh là ba đường chéo của đa giác đã cho.
HD: Chọn ra 3 đỉnh bất kỳ của đa giác có: cách chọn.
■ Số tam giác có 2 cạnh là cạnh của đa giác là: 10
(vì ứng với mỗi đỉnh ta lấy 2 cạnh kề với nó là được tgiác như điều kiện đã xét)
■ Số tam giác có 1 cạnh là cạnh của đa giác là: 10.6 = 60 vì chọn 1 cạnh của đa giác, ta chọn được 6 đỉnh để tạo tam giác (trừ đi 2 đỉnh của cạnh đó và 2 đỉnh nằm kề sát cạnh đó), mà có 10 cạnh như thế nên có 10.6 = 60
Suy ra số tgiác được tạo thành từ các đường chéo của đa giác là: 120 - 10 - 60 = 50 tam giác.