Tìm giá trị nguyên của tham số để phương trình có đúng hai nghiệm phân biệt.
A. 14
B. 15
C. 13
D. 16
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com

+) Để phương tình ban đầu có đúng hai nghiệm phân biệt thì phương trình bậc hai ẩn t hoặc có nghiệm kép t > 1 hoặc có 2 nghiệm phân biệt thỏa mãn

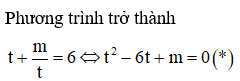
Để phương trình ban đầu có đúng hai nghiệm phân biệt thì phương trình (*)
TH1: Phương trình (*) có nghiệm kép t > 1
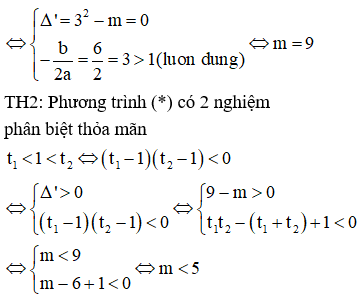
Kết hợp 2 TH và kết hợp điều kiện của bài toán ta có
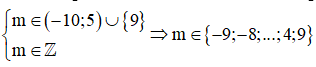
=> Có 15 giá trị của m thỏa mãn yêu cầu bài toán.
Chọn: B
Biết rằng phương trình có 4 nghiệm thực phân biệt. Hỏi phương trình sau có bao nhiêu nghiệm thực?
Hỏi hình tạo bởi 6 đỉnh là 6 trung điểm của các cạnh một tứ diện đều có bao nhiêu mặt phẳng đối xứng?
Cho tập hợp gồm 17 số nguyên dương đầu tiên. Chọn ngẫu nhiên một tập con có 3 phần tử của tập hợp S. Tính xác suất để tập hợp được chọn có tổng các phần tử chia hết cho 3.
Trong không gian cho tam giác ABC có . Dựng ở cùng một phía và vuông góc với mp (ABC). Tính khoảng cách từ trung điểm của A'C' đến mp (BCC')
Cho hàm số . Gọi S là tổng tất cả các giá trị của tham số m để đồ thị hàm số cắt đường thẳng tại ba điểm phân biệt sao cho tiếp tuyến của đồ thị hàm số tại B, C vuông góc với nhau. Giá trị của S bằng:
Cho hình chữ nhật ABCD, hình tròn xoay khi quay đường gấp khúc ABCD quanh cạnh AB trong không gian là hình nào dưới đây?
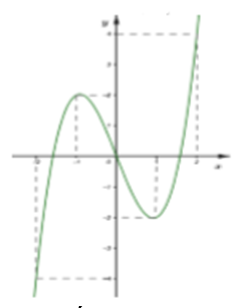
Cho hàm số có đồ thị hàm số là đường cong trong hình vẽ
bên. Mệnh đề nào dưới đây đúng?
Trong không gian với hệ trục tọa độ Oxyz, cho điểm . Gọi A, B, C lần lượt là hình chiếu vuông góc của điểm M trên các trục Ox, Oy, Oz. Viết phương trình mặt phẳng (ABC).
Gọi là hai điểm cực trị của hàm số . Tìm giá trị lớn nhất của biểu thức .
Cho x, y là các số thực thỏa mãn . Tìm giá trị nhỏ nhất của biểu thức
Cho hàm số f(x) có đạo hàm là . Hàm số f(x) đồng biến trên khoảng nào dưới đây?