Cho tứ giác ABCD. Gọi P, Q, R, S lần lượt là trung điểm của AB, AC, CD, DB.
1. Chứng minh tứ giác PQRS là hình bình hành.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
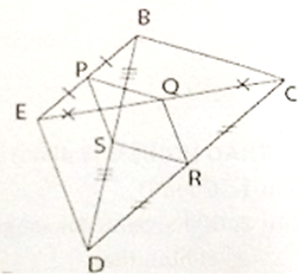
1) Ta có:
• PQ là đường trung bình của ΔABC nên PQ // BC và PQ = BC/2 (1)
• RS là đường trung bình của ΔDBC nên RS // BC và RS = BC/2 (2)
Từ (1) và (2) suy ra PQ // RS và PQ = RS
Suy ra tứ giác PQRS là hình bình hành.
Cho hình thoi ABCD. Gọi O là giao điểm hai đường chéo AC và BD. Đường thẳng qua O không song song với AD cắt AB tại M và CD tại N.
Cho tứ giác ABCD. Gọi P, Q, R, S lần lượt là trung điểm của AB, AC, CD, DB.
2. Tìm điều kiện của tứ giác ABCD để:
a. PQRS là hình chữ nhật.
Cho hình thang có hai đáy lần lượt là 3cm và 5cm. Độ dài đường trung bình là:
Cho tứ giác ABCD có BD là phân giác ∠B và BC = CD. Chứng minh tứ giác ABCD là hình thang.
Cho hình thoi ABCD. Gọi O là giao điểm hai đường chéo AC và BD. Đường thẳng qua O không song song với AD cắt AB tại M và CD tại N.
a) Chứng minh ΔAOM = ΔCON.
Cho tứ giác ABCD. Gọi P, Q, R, S lần lượt là trung điểm của AB, AC, CD, DB.
2. Tìm điều kiện của tứ giác ABCD để:
b. PQRS là hình thoi.
Phát biểu sau đúng hay sai: “Tứ giác có hai đường chéo bằng nhau và vuông góc với nhau là hình vuông”.
Hãy điền vào chỗ (…) để được các khẳng định đúng: b) Hình bình hành có ……… là hình chữ nhật.
Hãy điền vào chỗ (…) để được các khẳng định đúng: d) Tứ giác có ……… là hình thoi.
Hãy điền vào chỗ (…) để được các khẳng định đúng: c) ……… có hai đường chéo bằng nhau là hình vuông.
Hãy điền vào chỗ (…) để được các khẳng định đúng: a) Hình thang là tứ giác có ………