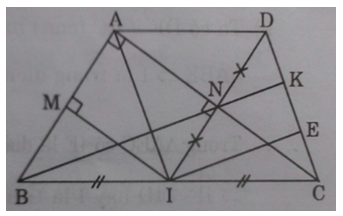
Cho tm giác ABC vuông tại A ( AB < AC). Gọi I là trung điểm của BC. Qua I vẽ IM ⊥ AB tại M, và IN ⊥ AC tại N.
b) Gọi D là điểm đối xứng của I qua N. Chứng minh ADCI là hình thoi.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
b) I là trung điểm của BC nên AI là đường trung tuyến của tam giác vuông ABC
⇒ AI = IC = BC/2. (1)
Do đó ΔAIC cân có IN là đường cao nên đồng thời là trung tuyến hay NA = NC (2)
lại có NI = NI (tính chất đối xứng) (3)
Từ (1), (2), (3) ⇒ ADIC là hình thoi.
Cho tm giác ABC vuông tại A ( AB < AC). Gọi I là trung điểm của BC. Qua I vẽ IM ⊥ AB tại M, và IN ⊥ AC tại N.
c) Đường thẳng BN cắt DC tại K. Chứng minh:
Cho hình thoi ABCD có O là giao điểm hai đường chéo. Gọi I là trung điểm cạnh BC và E là điểm đối xứng với O qua I.
b) Chứng tỏ E đối xứng với A qua trung điểm J của đoạn OB.
Cho hình thoi ABCD có O là giao điểm hai đường chéo. Gọi I là trung điểm cạnh BC và E là điểm đối xứng với O qua I.
a) Tứ giác OBEC là hình gì? Tại sao?
Cho tm giác ABC vuông tại A ( AB < AC). Gọi I là trung điểm của BC. Qua I vẽ IM ⊥ AB tại M, và IN ⊥ AC tại N.
a) Chứng minh AMIN là hình chữ nhật.
Cho hình thoi ABCD có Trên cạnh AD lấy điểm H và trên cạnh CD lấy điểm K sao cho AH = DK. Số đo góc ∠HBK là:
Cho hình thang ABCD (AB // CD), biết độ dài hai đáy AB = 10cm và CD = 22cm. Gọi H, K lần lượt là trung điểm của AD và BC. Độ dài đoạn thẳng HK là:
Cho ΔABC vuông tại A, đường cao AH. Gọi K và M lần lượt là hình chiếu của H trên AB và AC. Gọi N là trung điểm của CH. Số đo góc ∠KMN là:
Phần trắc nghiệm (3 điểm)
Chọn kết quả đúng: Trong tứ giác MNPQ có: