Cho tam giác ABC có , phân giác AD. Trên nửa mặt phẳng bờ là đường thẳng BC không chứa A. Dựng tia Bx tạo với BC một góc và cắt AD ở E. Chứng minh rằng:
a) ΔADC và ΔBDE đồng dạng và
b) ΔABD và ΔCED đồng dạng và ΔEBC đều
Giải bởi qa.haylamdo.com
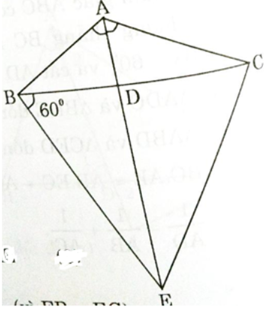
a) Xét ΔADC ∼ ΔBDE có:
∠DBE = ∠CAD ( = 60o)
∠BDE = ∠CDA (đối đỉnh)
⇒ ΔADC ∼ ΔBDE (g.g)
Xét ΔEBD và ΔEAB có:
∠BEA chung;
∠EBD = ∠BAE = 60o
⇒ ΔEBD ∼ ΔEAB (g.g)
b) Ta có ΔADC ∼ ΔBDE (cmt)
Lại có ∠ADB = ∠EDC (đối đỉnh)
Do đó ΔADB ∼ ΔCDE (c.g.c)
⇒ ∠BCE = ∠BAD = 60o
Vậy ΔEBC đều (∠EBC = ∠BCE = 60o )
c) Vì AD là phân giác của ∠BAC (gt) ta có:
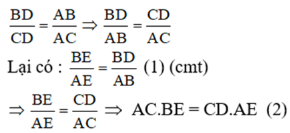
Từ (1) ta có AE.BD = BE.AB = EC.AB (vì EB = EC)
Hay EC.AB = AE.BD (3)
Công (2) và (3): AB.EC + AC.BE = AE(CD + BD) = AE.BC (đpcm)
d) Ta có: AE.BC = AB.EC + AC.BE
= AB.BC + AC.BC (vì BC = EC = BE)
= BC(AB + AC) ⇒ AE = AB + AC (*)
Mặt khác: Xét ΔADC và ΔABE có: ∠CAD = ∠BAE = 60o ; ∠ACD = ∠AEB (cmt)
⇒ ΔADC ∼ ΔABE (g.g)
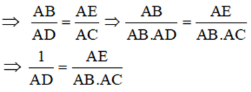
Theo (*) ta có:
Tam giác ABC cân tại A có , phân giác của góc B cắt AC tại M, phân giác của góc C cắt AB tại N.
a) Tính AM, CM và MN
b) Tính tỉ số diện tích của ΔAMN và ΔABC
Cho hình chữ nhật ABCD có Gọi M là trung điểm BC, đường thẳng AM cắt CD tại N. Độ dài MN là:
Cho hình bình hành ABCD. Qua A vẽ một đường thẳng sao cho đường thẳng này cắt BD, BC lần lượt tại K và M, cắt đường DC tại N. Khi đó bằng
Cho tam giác ABC có AB = 6cm; BC = 9cm. Kẻ BD là phân giác trong của ∠ABC . Qua D kẻ đường thẳng song song với BC cắt AB tại E. Khi đó:
Cho ΔDEF ∼ ΔABC biết DE = 5cm, AB = 6cm, AC = 12cm. Độ dài DF là:
