Cho hình hộp chữ nhật ABCD.EFGH. Chứng tỏ rằng:
a) ACGE là hình chữ nhật
b) DF = CE
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
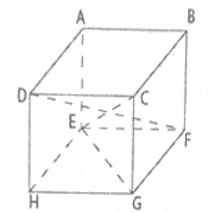
a) Ta có AE // CG; AE = CG (gt)
Tứ giác ACGE là hình bình hành
Mặt khác AE ⊥ mp(EFGH)
Mà EG ⊂ mp(EFGH) => AE ⊥ EG tại E
Vậy tứ giác ACGE là hình chữ nhật
b) Chứng minh DF = CE
Vì DH ⊥ mp(EFGH ) nên DH ⊥ HF tại H
Suy ra DF2 = DH2 + HF2(Py-ta-go) (1)
Vì AE ⊥ mp(ABCD) nên AE ⊥ AC tại A
Suy ra CE2 = AE2 + AC2(Py-ta-go) (2)
Mà DH = AE; HF = EG = AC (hai đường chéo của hình chữ nhật) (3)
Từ (1), (2) và (3) suy ra DF2 = CE2 => DF = CE
Cho hình chóp tứ giác đều S.ABCD, đáy ABCD là hình vuông có cạnh 3cm, cạnh bên SA = 5cm.
a) Tính đường cao SH của hình chóp.
b) Tính diện tích xung quanh và thể tích của hình chóp.
Một hình chóp tứ giác đều có thể tích bằngchiều cao của hình chóp là 8cm. Độ dài cạnh đáy của hình chóp bằng:
Cho hình hộp chữ nhật ABCD.MNPQ có chiều dài chiều rộng chiều cao Thể tích hình hộp chữ nhật ABCD.MNPQ là:
Diện tích toàn phần của một hình lập phương là Thể tích của hình lập phương này là:
Cho hình hộp chữ nhật ABCD.EFGH. Số các cặp mặt phẳng song song với nhau là: