a) Chứng minh: Tứ giác AEHF là hình chữ nhật.
b) Gọi P là điểm đối xứng của H qua AB. Tứ giác APEF là hình gì? Vì sao?
c) Đường thẳng đi qua C và song song với BP, cắt tia PA tại Q. Chứng minh: Q đối xứng với H qua F.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Hướng dẫn giải
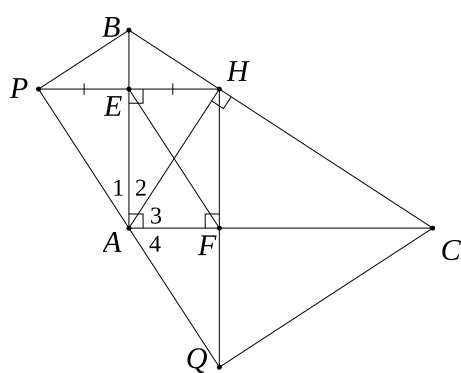
a) Tứ giác AEHF có:
\(\widehat A = 90^\circ \) (tam giác ABC vuông tại A)
HE ⊥ AB ⇒ \(\widehat {AEH} = 90^\circ \)
HF ⊥ AC ⇒ \(\widehat {AFH} = 90^\circ \)
⇒ Tứ giác AEHF là hình chữ nhật (tứ giác có 3 góc vuông)
b) Hình chữ nhật AEHF có:
EH // AF và EH = AF
Lại có: PE = EH (vì P là điểm đối xứng của H qua AB)
⇒ PE = AF (= EH)
Tứ giác APEF có:
EP // AF và PE = AF
⇒ Tứ giác APEF là hình bình hành. (Tứ giác có hai cạnh đối song song và bằng nhau)
c) Vì P đối xứng với H qua AB nên AB là đường trung trực của PH
⇒ AP = AH và BP = BH
Xét ΔAPB và ΔAHB có:
BP = PH
AP =AH
AB chung
⇒ ΔAPB = ΔAHB (c.c.c)
\( \Rightarrow \widehat {{A_1}} = \widehat {{A_2}}\) và \(\widehat {APB} = \widehat {AHB}\) (hai góc tương ứng)
Mà có \(\widehat {AHB} = 90^\circ \) nên \(\widehat {APH} = 90^\circ \)
Hay AP ⊥ PB
Ta có AP ⊥ PB và PB // CQ
⇒ AP ⊥ CQ hay AQ ⊥ CQ \( \Rightarrow \widehat {AQC} = 90^\circ \).
Ta có: \[\left\{ \begin{array}{l}\widehat {{A_4}} + \widehat {{A_1}} = 180^\circ - \widehat {BAC} = 90^\circ \\\widehat {{A_3}} + \widehat {{A_4}} = \widehat {BAC} = 90^\circ \end{array} \right.\] và \(\widehat {{A_1}} = \widehat {{A_2}}\) (cmt)
\( \Rightarrow \widehat {{A_3}} = \widehat {{A_4}}\)
Xét ΔAHC và ΔAQC có:
\(\widehat {{A_3}} = \widehat {{A_4}}\) (cmt)
AC chung
\(\widehat {AHC} = \widehat {AQC} = 90^\circ \)
⇒ ΔAHC = ΔAQC (cạnh huyền góc nhọn)
⇒ AH = AQ (hai cạnh tương ứng)
Xét ΔAHF và ΔAQF có:
\(\widehat {{A_3}} = \widehat {{A_4}}\) (cmt)
AF chung
AH = AQ (cmt)
⇒ ΔAHF = ΔAQF (c.g.c)
\( \Rightarrow \widehat {AFH} = \widehat {AFQ}\) (hai góc tương ứng)
Mà \(\widehat {AFH} = 90^\circ \) nên \(\widehat {AFQ} = 90^\circ \).
Ta có: \(\widehat {HFQ} = \widehat {AFH} + \widehat {AFQ} = 90^\circ + 90^\circ = 180^\circ \)
Hay H, F, Q thẳng hàng (1)
Vì ΔAHF = ΔAQF (cmt) nên HF = QF (2)
Từ (1) và (2) suy ra Q đối xứng với H qua F.
a) Thực hiện phép chia đa thức A cho đa thức B. Xác định đa thức thương M và phần dư N.
b) Tìm tất cả các số nguyên x để giá trị của đa thức A chia hết cho giá trị của đa thức B (trên ℤ).
a) x(5 – 6x) + (2x – 1)(3x + 4) = 6;
b) x2(x – 2021) – x + 2021 = 0;
c) 2x2– 3x – 5 = 0.
Phân tích các đa thức sau thành nhân tử:
a) A = 4x3– 8x2+ 4x;
b) B = y2+ x2– 16 – 2xy;
c) C = x3– 8 – 3(2 – x).