Cho hàm số y = f(x) có bảng biến thiên như sau:
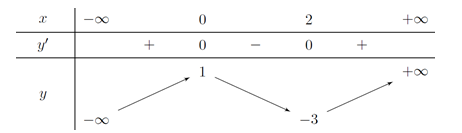
Số nghiệm thực phân biệt của phương trình là
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Chọn A.
Ta có:
Phương trình (*) chính là phương trình hoành độ giao điểm của đồ thị hàm số y = f(x) và đường thẳng
Số nghiệm của phương trình chính là số giao điểm của đồ thị hàm số y = f(x) và đường thẳng
Ta có bảng biến thiên
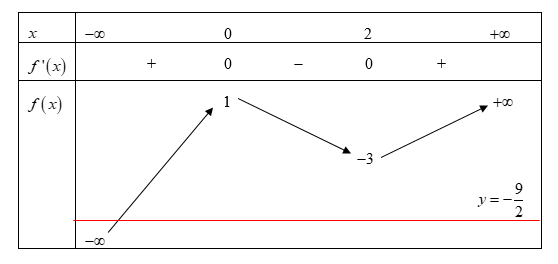
Dựa vào bảng biến thiên ta thấy đường thẳng cắt đồ thị hàm số y = f(x) tại 1 điểm nên phương trình có 1 nghiệm.
Cho hình bát diện đều cạnh 4a. Gọi S là tổng diện tích của tất cả các mặt của hình bát diện đều đó. Khi đó S bằng:
Chọn ngẫu nhiên một số từ tập các số tự nhiên có năm chữ số đôi một khác nhau. Xác suất để số được chọn có mặt đồng thời cả ba chữ số 1, 2 và 3 là
Cho hàm số y= f(x) liên tục trên đoạn [-3; 4] và có đồ thị như hình vẽ.
![Cho hàm số y= f(x) liên tục trên đoạn [-3; 4] và có đồ thị như hình vẽ. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/04/blobid0-1650090758.png)
Gọi M và m lần lượt là các giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn [-3; 1]. Tích M.n bằng
Trong không gian Oxyz, hình chiếu vuông góc của điểm A(2; 3; 4) trên trục Oz có tọa độ là
Cho hình chóp S.ABCD có và Tính thể tích V của khối chóp S.ABCD.