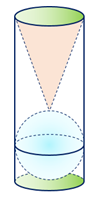
Trên bàn có một cốc nước hình trụ chứa đầy nước, có chiều cao bằng 3 lần đường kính của đáy; một viên bi và một khối nón đều bằng thủy tinh. Biết viên bi là một khối cầu có đường kính bằng của cốc nước. Người ta từ từ thả vào cốc nước viên bi và khối nón đó (như hình vẽ) thì thấy nước trong cốc tràn ra ngoài. Tính tỉ số thể tích của lượng nước còn lại trong cốc và lượng nước ban đầu (bỏ qua bề dày của lớp vỏ thủy tinh).

Hỗn hợp E gồm hai chất: X $\left(C_n{H}_{2n+4}{O}_4{N}_2\right)$ là muối amoni của axit cacboxylic hai chức, chất Y $\left(C_m{H}_{2m+4}{O}_2{N}_2\right)$ là muối amoni của một amoni axit với amin, n > m. Cho 0,1 mol hỗn hợp E tác dụng với lượng dư dung dịch KOH, đun nóng, thu được 17,56 gam hỗn hợp hai muối và 3,584 lít hỗn hợp khí Z (đktc) gồm hai amin kế tiếp nhau, tỉ khối với H₂ là 18,125. Phần trăm khối lượng của X trong E là

Cho các nhận định sau:

(a) Muối natri cacbonat là nguyên liệu trong công nghiệp sản xuất thủy tinh, xà phòng.

(b) Thạch cao nung (CaSO₄.H₂O) được dùng làm phấn viết bảng, bó bột khi gãy xương.

(c) Nhôm và hợp kim của nhôm được dùng làm khung cửa và trang trí nội thất.

(d) Oxit sắt (III) được dùng để pha sơn chống gỉ.

(e) KCr(SO₄)₂.14H₂O được dùng làm chất cầm màu trong ngành nhuộm vải.

Số nhận định đúng là

Thủy phân hoàn toàn chất hữu cơ X (C₈H₁₂O₄, chứa 2 chức este) bằng dung dịch NaOH, thu được sản phẩm gồm ancol Z và hỗn hợp Y gồm hai muối. Axit hóa Y thu được hai axit cacboxylic Y₁ và Y₂ có cùng số nguyên tử hiđro $\left(M_{Y_1}>M_{Y_2}\right).$  Cho các phát biểu sau:

(a) Phân tử khối của Z là 62 g/mol.

(b) Có 3 công thức cấu tạo thỏa mãn tính chất của X.

(c) Nung nóng muối natri của Y₂ với hỗn hợp rắn gồm NaOH và CaO, thu được CH₄.

(d) Chất Y₁ bị oxi hóa bởi dung dịch Br₂.

Số phát biểu đúng là

Hòa tan hết 27,2 gam hỗn hợp rắn X gồm Fe₃O₄, Fe₂O₃ và Cu trong dung dịch chứa 0,9 mol HCl (dùng dư), thu được dung dịch Y có chứa 13,0 gam FeCl₃. Tiến hành điện phân dung dịch Y bằng điện cực trơ đến khi catot bắt đầu có khí thoát ra thì dừng điện phân, thấy khối lượng dung dịch giảm 13,64 gam. Cho dung dịch AgNO₃ dư vào dung dịch sau điện phân, kết thúc phản ứng thấy khí NO thoát ra (sản phẩm khử duy nhất), đồng thời thu được m gam kết tủa. Giá trị của m là

Tiến hành thí nghiệm theo các bước sau đây:

Bước 1: Dùng 4 kẹp sắt kẹp 4 vật liệu riêng lẻ: mẫu màng mỏng PE, mẫu ống nhựa dẫn nước làm bằng PVC, sợi len (làm từ lông cừu) và vải sợi xenlulozơ (hoặc bông).

Bước 2: Hơ các vật liệu này (từng thứ một) ở gần ngọn lửa vài phút.

Bước 3: Đốt các vật liệu trên.

Cho các nhận định sau:

(a) PVC bị chảy ra trước khi cháy, cho nhiều khói đen, khí thoát ra có mùi xốc khó chịu.

(b) Sợi len cháy mạnh, khí thoát ra không có mùi khét.

(c) PE bị chảy ra thành chất lỏng, sản phẩm cháy tạo hoàn toàn thành khí, không có chất lỏng hay rắn.

(d) Sợi vải cháy mạnh, khí thoát ra không có mùi.

(e) Khi hơ nóng 4 vật liệu: PVC bị chảy ra, PE bị chảy thành chất lỏng.

Số nhận định không đúng là

Cho m gam hỗn hợp X gồm K₂O, Ba vào dung dịch chứa 0,06 mol HCl và 0,08 mol BaCl₂ thu được x mol khí và dung dịch Y. Hấp thụ từ từ CO₂ vào dung dịch Y ta có đồ thị sau:

Giá trị của m là

Hỗn hợp E gồm etyl axetat, metyl fomat, phenyl fomat và một số trieste của glyxerol với các axit no, hở, đơn chức (biết số mol phenyl fomat = số mol etyl axetat + số mol metyl fomat). Lấy 0,09 mol E đem đốt cháy hoàn toàn cần dùng 0,675 mol O₂ thu được 0,43 mol H₂O. Nếu lấy 51,92 gam E thì tác dụng hết với dung dịch chứa 0,8 mol KOH. Làm bay hơi dung dịch sau phản ứng thu được m gam chất rắn X và phần hơi chứa 16 gam các chất hữu cơ. Thành phần % khối lượng của kaliphenolat trong X là

Tiến hành điện phân dung dịch chứa Cu(NO₃)₂ 1,2M và NaCl 0,8M bằng điện cực trơ, sau một thời gian thấy khối lượng dung dịch giảm 17,7 gam. Cho 0,18 mol bột Fe vào dung dịch sau điện phân, kết thúc phản ứng, thấy thoát ra 0,06 mol khí NO (sản phẩm khử duy nhất); đồng thời còn lại x gam rắn không tan. Giá trị x là

Cho các nhận định sau:

(a) Triolein là hợp chất hữu cơ đa chức.

(b) Glucozơ cho được phản ứng tráng gương.

(c) Dung dịch metylamin không làm hồng dung dịch phenolphtalein.

(d) Poliacrilonitrin thuộc tơ tổng hợp.

(e) Sau khi mổ cá, có thể dùng giấm ăn để giảm mùi tanh.

(g) Thành phần chính của bông nõn là xenlulozơ.

Các nhận định đúng là

Hòa tan hết 26,43 gam hỗn hợp bột X gồm Mg, Al, Al₂O₃ và MgO bằng 795 ml dung dịch hỗn hợp gồm HCl 0,5M và H₂SO₄ 0,75M (vừa đủ). Sau phản ứng thu được dung dịch Y và 4,368 lít khí H₂ (ở đktc). Cô cạn dung dịch Y thu được khối lượng muối khan là