A. Đồ thị hàm số y=ax và đồ thị hàm số y=logax đối xứng nhau qua đường thẳng y = x.
B. Hàm số y=ax với 0 < a < 1 đồng biến trên khoảng (−∞;+∞).
C. Đồ thị hàm số y=ax với a>0;a≠1 luôn đi qua điểm M(a; 1).
D. Hàm số y=ax với a > 1 nghịch biến trên khoảng (−∞;+∞).
Giải bởi qa.haylamdo.com
Phương pháp:
Áp dụng các tính chất hàm số mũ và hàm logarit.
Cách giải:
Hàm số y=ax đồng biến trên ℝ khi a > 1 và nghịch biến trên ℝ khi 0 < a < 1 nên các đáp án B, D sai.
Với a>0;a≠1 thì đồ thị hàm số không luôn đi qua M(a; 1) nên đáp án C sai.
Chọn A.
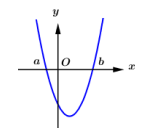
Cho hàm số bậc ba y = f(x) có đồ thị của hàm số f'(x) như hình vẽ và f(b) = 1. Số giá trị nguyên của m∈[−5;5] để hàm số g(x)=|f2(x)+4f(x)+m| có đúng 5 điểm cực trị là:
Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình x4+16x4+4(x2+4x2)−12(x−2x)−m=0 có nghiệm thuộc [1; 2]?
Hàm số y = f(x) liên tục trên [2; 9]. F(x) là một nguyên hàm của hàm số f(x) trên [2; 9] và F(2)=5,F(9)=4. Mệnh đề nào sau đây đúng?
Cho hàm số y = f(x) có đạo hàm f'. Số điểm cực tiểu của hàm số đã cho là
Tìm tất cả các giá trị thực của tham số m để hàm số đồng biến trên khoảng
