Cho đồ thị hàm số y = f'(x) như hình vẽ, biết Hỏi có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số có đúng bốn điểm cực trị?
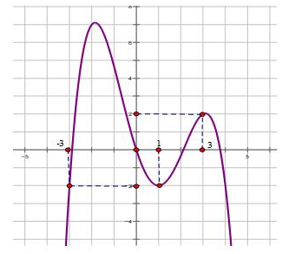
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Chọn D.
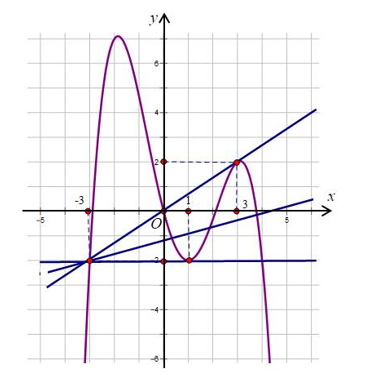
Xét hàm số
Ta có:
Đặt suy ra (*) có dạng:
Số nghiệm bội lẻ của phương trình g'(x) = 0 bằng với số nghiệm bội lẻ của phương trình tương đương với số giao điểm không tiếp xúc của hai đồ thị y = f'(t) và đường thẳng
Đường thẳng d luôn đi qua A(-3; -2)
Gọi là đường thẳng đi qua A và tiếp xúc với đồ thị hàm số y = f'(t) tại điểm (3; 2) như hình vẽ.
Suy ra: khi đó giá trị tham số thỏa mãn
Gọi là đường thẳng đi qua A và tiếp xúc với đồ thị hàm số y = f'(t) tại điểm (1; -2) như hình vẽ.
Suy ra: khi đó giá trị tham số thỏa mãn
Để hàm số g(x) có bốn điểm cực trị thì phương trình có bốn nghiệm bội lẻ, tương đương với đồ thị y = f'(t) và đường thẳng d có bốn giao điểm xuyên qua.
Do đó

Trong không gian với hệ trục tọa độ Oxyz cho ba điểm Tâm mặt cầu ngoại tiếp tứ diện OABC có tọa độ I(a; b;c) tổng a + b + c bằng
Cho phương trình Hỏi có bao nhiêu cặp thỏa mãn phương trình đã cho
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là
Cho phương trình có một nghiệm là 3 + 4i. Giá trị của biểu thức a + b bằng
Cho phương trình (m là tam số thực). Số giá trị nguyên của m để phương trình đã cho có đúng 2 nghiệm phân biệt thuộc khoảng (0; 1)
Cho hàm số f(x) có bảng biến thiên như sau
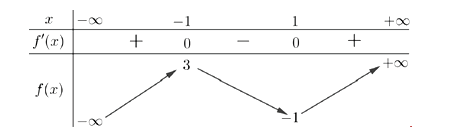
Số nghiệm của phương trình 3f(x) - 2 = 0 là