Cho hàm số f(x)=x3+3x2−2m+1 (m là tham số thực). Gọi S là tập hợp tất cả các giá trị của m sao cho max[1;3]|f(x)|+min[1;3]|f(x)|≥10. Số các giá trị nguyên của S trong đoạn [-30; 30) là
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Chọn A.
Ta có f' nên hàm số f(x) đồng biến trên đoạn [1; 3] tức là f(1) < f(3).
Lại có Ta xét các trường hợp:
+) Trường hợp 1:
Khi đó nên từ yêu cầu bài toán suy ra
Kết hợp có
+) Trường hợp 2:
Khi đó
Nếu thì nên từ yêu cầu bài toán suy ra Kết hợp m < 15 suy ra m < 15 (*)
Nếu thì nên từ yêu cầu bài toán suy ra Kết hợp suy ra (**)
Kết hợp (*) và (**) với có
+) Trường hợp 3:
Khi đó và nên từ yêu cầu bài toán suy ra
Kết hợp có (3)
Từ (1), (2), (3) suy ra tập
Vậy số các giá trị nguyên của S trong đoạn [-30; 30] là 61.
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1; 0; 2) và đường thẳng d có phương trình: Viết phương trình đường thẳng đi qua A vuông góc và cắt d.
Cho khối hộp chữ nhật ABCD.A'B'C'D' có Bán kính mặt cầu ngoại tiếp khối hộp chữ nhật đã cho bằng
Trong không gian với hệ trục tọa độ Oxyz, phương trình mặt cầu (S) nhận gốc tọa độ O làm tâm và đi qua điểm M(2; 0; 0) là
Tìm tất cả các giá trị thực của tham số m sao cho hàm số luôn nghịch biến trên các khoảng xác định của nó?
Cho hàm số y = f(x) liên tục trên , hàm số f'(x) có đồ thị như hình vẽ bên dưới.
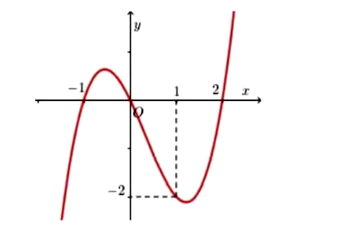
Hàm số đạt giá trị lớn nhất trên [-2;2] bằng
Cho khối lập phương có thể tích bằng 125. Độ dài cạnh của khối lập phương đã cho bằng
Cho tập hợp A gồm 9 phần tử. Số tập con gồm có 4 phần tử của tập A là
Trong không gian Oxyz hình chiếu vuông góc của điểm M(2; -1; 1) trên trục Ox có tọa độ là
Xét tất cả các số thực dương a, b và c thỏa mãn Mệnh đề nào dưới đây đúng?
Cho khối chóp S.ABC có và SA = 2, tam giác ABC vuông cân tại A và AB = 1. Thể tích khối chóp S.ABC bằng
Một hình nón có thể tích bằng và bán kính của đường tròn đáy bằng 2a. Khi đó, đường cao của hình nón là: