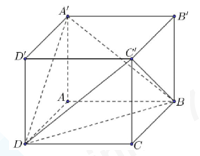
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có đáy ABCD là hình vuông cạnh \(a\sqrt 2 \) cạnh bên AA′=a (minh họa như hình vẽ). Góc giữa hai mặt phẳng (A′BD) và (C′BD) bằng bao nhiêu độ?
Giải bởi qa.haylamdo.com
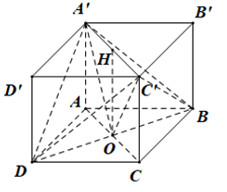
Bước 1: Xác định góc
Vì ABCD là hình vuông nên AC vuông góc BD tại O.
Suy ra \[BD \bot \left( {A'OC'} \right)\]. Góc giữa hai mặt phẳng\[\left( {A'BD} \right),\,\,\left( {C'BD} \right)\] là\[\angle A'OC'\]
Bước 2: Sử dụng tính chất tam giác vuông cân để tính góc.
Gọi H là tâm hình vuông A′B′C′D′ thì H là trung điểm A′C′ và\[\begin{array}{*{20}{l}}{OH = A'A = a}\\{A'H = HC' = \frac{{A'C'}}{2} = \frac{{A'B'\sqrt 2 }}{2} = \frac{{a\sqrt 2 .\sqrt 2 }}{2} = a}\end{array}\]
Suy ra các tam giác\[OHA';\,\,OHC'\] vuông cân và\[\angle A'OC' = {90^ \circ }\]
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a. Đường thẳng SO vuông góc với mặt phẳng đáy (ABCD) và \(SO = \frac{{a\sqrt 3 }}{2}\). Tính góc giữa hai mặt phẳng (SBC) và (ABCD).
Trong không gian cho tam giác đều SAB và hình vuông ABCD cạnh a nằm trên hai mặt phẳng vuông góc. Gọi H, K lần lượt là trung điểm của AB, CD. Gọi φ là góc giữa hai mặt phẳng (SAB) và (SCD). Mệnh đề nào sau đây đúng?
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên SA=x và vuông góc với mặt phẳng (ABCD). Xác định x để hai mặt phẳng (SBC) và (SCD) tạo với nhau một góc 600.
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân, AB=BC=2a. Tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với (ABC), \(SA = \sqrt 3 a\). Góc giữa hai mặt phẳng (SAB) và (SAC) bằng:
Cho hình chóp S.ABC có đáy ABC. là tam giác vuông tại B, BC=a. Cạnh bên SA=a vuông góc với mặt phẳng đáy. Góc giữa hai mặt phẳng (SBC) và (ABC) bằng \[{45^0}\]. Độ dài AC bằng
Cho hình chóp S.ABCD có đáy là hình thang vuông ABCD vuông tại A và D, AB=2a, AD=CD=a. Cạnh bên SA=a và vuông góc với mặt phẳng (ABCD). Gọi \[\varphi \] là góc giữa hai mặt phẳng (SBC) và (ABCD) . Mệnh đề nào sau đây đúng?
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại C. Gọi H là trung điểm AB. Biết rằng SH vuông góc với mặt phẳng (ABC) và AB=SH=a. Tính cosin của góc α tọa bởi hai mặt phẳng (SAB) và (SAC).
Cho hình lăng trụ tứ giác đều ABCD.A′B′C′D′ có đáy cạnh bằng a, góc giữa hai mặt phẳng (ABCD) và (ABC′) có số đo bằng \({60^0}\). Độ dài cạnh bên của hình lăng trụ bằng
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, cạnh bên SA vuông góc với đáy. Gọi E,F lần lượt là trung điểm của cạnh AB và AC. Góc giữa hai mặt phẳng (SEF) và (SBC) là
Cho hai tam giác ACD và BCD nằm trên hai mặt phẳng vuông góc với nhau và AC=AD=BC=BD=a,CD=2x. Với giá trị nào của x thì hai mặt phẳng (ABC) và (ABD) vuông góc.
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, các cạnh \[SA = SB = a,\;SD = a\sqrt 2 \]. Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng \({90^0}\). Độ dài đoạn thẳng BD
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh aa. Cạnh bên \(SA = a\sqrt 3 \) và vuông góc với mặt đáy (ABC). Gọi φ là góc giữa hai mặt phẳng (SBC) và (ABC). Mệnh đề nào sau đây đúng?
Cho hình chóp đều S.ABCD có tất cả các cạnh bằng aa. Gọi M là trung điểm SC. Tính góc \[\varphi \] giữa hai mặt phẳng (MBD) và (ABCD).
Trong mặt phẳng (P) cho tam giác đều ABC cạnh a. Trên các đường thẳng vuông góc với mặt phẳng (P) tại B và C lấy điểm D,E cùng phía so với (P) sao cho \(BD = \frac{{a\sqrt 3 }}{2}\) và \(CE = a\sqrt 3 \).Tính góc giữa hai mặt phẳng (ADE) và (ABC).
