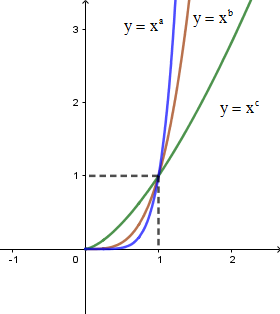
Cho đồ thị của ba hàm số \[y = {x^a};y = {x^b};y = {x^c}\] trên khoảng \[\left( {0; + \infty } \right)\;\]trên cùng một hệ trục tọa độ như hình vẽ bên. Mệnh đề nào sau đây đúng?
A.c<b<a<0
</b<a<0 >
B.0<c<b<a<1
</c<b<a<1
C.1<c<b<a
</c<b<a
D.0<a<b<c<1
</a<b<c<1
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
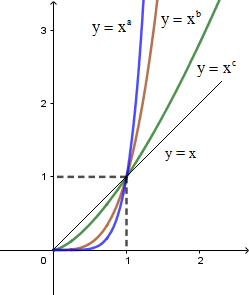
Từ đồ thị hàm số ta thấy:
- Với 0<x<1 thì \[{x^a} < {x^b} < {x^c} < {x^1} \Leftrightarrow a > b > c > 1\]</x
- Với x>1 thì \[x < {x^c} < {x^b} < {x^a} \Rightarrow 1 < c < b < a\]
Vậy 1<c<b<a
Đáp án cần chọn là: C
Cho hàm số \[y = {x^\alpha }\]. Nếu \[\alpha = 1\;\] thì đồ thị hàm số là:
Đẳng thức \[{\left( {\sqrt[n]{x}} \right)^\prime } = ({x^{\frac{1}{n}}})' = \frac{1}{n}{x^{ - \frac{{n - 1}}{n}}} = \frac{1}{{n\sqrt[n]{{{x^{n - 1}}}}}}\] xảy ra khi:
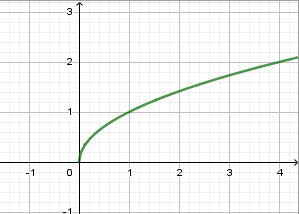
Xét hàm số \[y = {x^\alpha }\] trên tập \[\left( {0; + \infty } \right)\;\]có đồ thị dưới đây, chọn kết luận đúng:
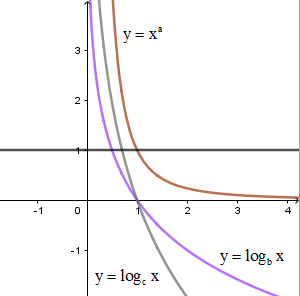
Cho aa là số thực tùy ý và b,c là các số thực dương khác 1. Hình vẽ bên là đồ thị của ba hàm số \[y = lo{g_b}x;y = lo{g_c}x;y = {x^a}(x > 0)\] Khẳng định nào sau đây đúng?
Cho hàm số \[y = {x^{e - 3}}\]. Trong các kết luận sau kết luận nào sai?
Cho hàm số \[y = {\left( {x + 2} \right)^{ - 2}}\]. Hệ thức giữa y và y″ không phụ thuộc vào x là:
Trên đồ thị (C) của hàm số \(y = {x^{\frac{\pi }{2}}}\) lấy điểm M0 có hoành độ x0=1. Tiếp tuyến của (C) tại điểm M0 có phương trình là:
Tìm TXĐ của hàm số \[y = {\left( {{x^3} - 27} \right)^{\frac{\pi }{2}}}\]
Tính đạo hàm của hàm số \[y = {\left( {2{x^2} + x - 1} \right)^{\frac{2}{3}}}\].
Cho aa là số thực tùy ý và b,c là các số thực dương khác 1. Hình vẽ bên là đồ thị của ba hàm số \[y = lo{g_b}x;y = lo{g_c}x;y = {x^a}(x > 0)\] Khẳng định nào sau đây đúng?
