Xác định tập nghiệm S của bất phương trình $\ln {x^2} > \ln \left( {4x - 4} \right)$

Có tất cả bao nhiêu giá trị nguyên của y sao cho tương ứng với mọi y luôn tồn tại không quá 63 số nguyên x thỏa mãn điều kiện ${\log _{2020}}\left( {x + {y^2}} \right) + {\log _{2021}}\left( {{y^2} + y + 64} \right) \ge {\log _4}\left( {x - y} \right)$

Cho phương trình ${11^x} + m = {\log _{11}}\left( {x - m} \right)$ với m là tham số. Có bao nhiêu giá trị nguyên của $m \in \left( { - 205;205} \right)\;$ để phương trình đã cho có nghiệm?

Xét bất phương trình $\log _2^22x - 2\left( {m + 1} \right){\log _2}x - 2 < 0$. Tìm tất cả các giá trị của tham số m để bất phương trình có nghiệm thuộc khoảng $\left( {\sqrt 2 ; + \infty } \right).$

Tập nghiệm của bất phương trình $\log \left( {{x^2} + 25} \right) > \log \left( {10x} \right)$ là:

Tập nghiệm của bất phương trình${\log _2}\left( {x\sqrt {{x^2} + 2} + 4 - {x^2}} \right) + 2x + \sqrt {{x^2} + 2} \le 1$ là $\left( { - \sqrt a ; - \sqrt b } \right)$.Khi đó abab bằng

Tập nghiệm của bất phương trình ${9^{\log _9^2x}} + {x^{{{\log }_9}x}} \le 18$là:

Bất phương trình  ${\log _{\frac{4}{{25}}}}(x + 1) \ge {\log _{\frac{2}{5}}}x$ tương đương với bất phương trình nào dưới đây?

Tập hợp nghiệm của bất phương trình ${\log _{\frac{1}{3}}}\left( {{x^2} - 2x + 1} \right) < {\log _{\frac{1}{3}}}\left( {x - 1} \right)$ là:

Tập nghiệm của bất phương trình ${\left( {\sqrt 5 - 2} \right)^{\frac{{2x}}{{x - 1}}}} \le {\left( {\sqrt 5 + 2} \right)^x}$ là:

Số nguyên nhỏ nhất thỏa mãn ${\log _2}\left( {5x - 3} \right) > 5$ là:

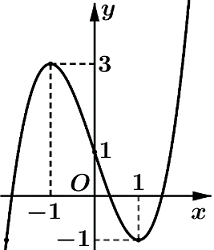
Cho hàm số y=f(x). Hàm số y=f′(x) có đồ thị như hình bên. Biết $f\left( { - 1} \right) = 1,f( - \frac{1}{e}) = 2.$. Tìm tất cả các giá trị của m để bất phương trình $f(x) < ln( - x) + m\;$ nghiệm đúng với mọi $x \in ( - 1; - \frac{1}{e}).$

Tập nghiệm của phương trình ${\log _3}\left( {{{\log }_{\frac{1}{2}}}x} \right) < 1$ là

Cho $m = {\log _a}\sqrt {ab}$ với a,b>1 và $P = \log _a^2b + 54{\log _b}a$. Khi đó giá trị của m để P đạt giá trị nhỏ nhất là:

Tìm tập nghiệm S của bất phương trình ${\log _{\frac{1}{2}}}\left( {x - 1} \right) > {\log _{\frac{1}{2}}}\left( {5 - 2x} \right)$