Xét số phức z thỏa mãn \[\left| {z + 2 - i} \right| + \left| {z - 4 - 7i} \right| = 6\sqrt 2 \]. Gọi m,M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của \[\left| {z - 1 + i} \right|.\]Tính P=m+M.
A.\[P = \sqrt {13} + \sqrt {73} \]
B. \[P = \frac{{5\sqrt 2 + 2\sqrt {73} }}{2}\]
C. \[P = 5\sqrt 2 + \sqrt {73} \]
D. \[P = \frac{{5\sqrt 2 + \sqrt {73} }}{2}\]
Giải bởi qa.haylamdo.com
Gọi \[z = x + yi\left( {x,y \in R} \right)\]
Trên mặt phẳng tọa độ Oxy gọi P(x;y) là điểm biểu diễn của số phức z
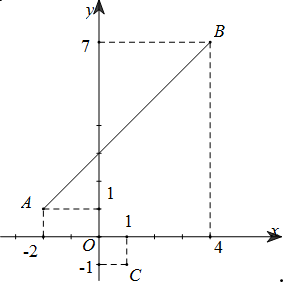
Gọi \[A\left( { - 2;1} \right),B\left( {4;7} \right)\]thì
\[\begin{array}{*{20}{l}}{AB = 6\sqrt 2 = \left| {z + 2 - i} \right| + \left| {z - 4 - 7i} \right|}\\{ = \sqrt {{{\left( {x + 2} \right)}^2} + {{\left( {y - 1} \right)}^2}} + \sqrt {{{\left( {x - 4} \right)}^2} + {{\left( {y - 7} \right)}^2}} = PA + PB}\end{array}\]
Suy ra tập hợp các điểm P thỏa mãn chính là đoạn thẳng AB
Có\[\left| {z - 1 + i} \right| = \sqrt {{{\left( {x - 1} \right)}^2} + {{\left( {y + 1} \right)}^2}} = PC\]với C(1;−1)
Do đó\[P{C_{\min }}\]khi P là hình chiếu của C lên AB và \[P{C_{\max }}\] khi\[P \equiv B\]
Suy ra \[M = CB = \sqrt {73} \]
Ta có:\[AB:\frac{{x + 2}}{{4 + 2}} = \frac{{y - 1}}{{7 - 1}} \Leftrightarrow x - y + 3 = 0\]
\[ \Rightarrow m = d\left( {C,AB} \right) = \frac{{\left| {1 - \left( { - 1} \right) + 3} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} }} = \frac{5}{{\sqrt 2 }}\]
\[ \Rightarrow M + m = \frac{{5\sqrt 2 + 2\sqrt {73} }}{2}\]
Đáp án cần chọn là: B
Tìm các số thực x,y thỏa mãn đẳng thức \[3x + y + 5xi = 2y - (x - y)i.\]
Cho hai số phức \[{z_1},\,\,{z_2}\] thỏa mãn \[{z_1}\overline {.{z_1}} = 4,\left| {{z_2}} \right| = 3\]. Giá trị biểu thức \[P = {\left| {{z_1}} \right|^2} + {\left| {{z_2}} \right|^2}\;\] bằng:
Cho \[{z_1} = 2 + i;\,\,{z_2} = 1 - 3i.\]. Tính \[A = {\left| {{z_1}} \right|^2} + {\left| {{z_2}} \right|^2}.\]
Tính môđun của số phức \[w = {\left( {1 - i} \right)^2}z\], biết số phức z có môđun bằng m.
Cho số phức z thỏa mãn \[2iz + \overline z = 1 - i.\]Phần thực của số phức z là:
Cho số phức \[z = 3 - 2i\]. Tìm phần thực và phần ảo của số phức \(\overline z \)
Gọi M,N lần lượt là các điểm biểu diễn số phức \[z = a + bi\] và \[z\prime = a\prime + b\prime i\]. Chọn câu đúng:
Trên C phương trình \[\frac{2}{{z - 1}} = 1 + i\;\] có nghiệm là:
Tính môđun của số phức z biết \[\bar z = \left( {4 - 3i} \right)\left( {1 + i} \right)\]
