Viết phương trình mặt phẳng (P) song song với mặt phẳng \[\left( Q \right):x + y - z - 2 = 0\;\]và cách (Q) một khoảng là \(2\sqrt 3 \).
A.\[x + y - z + 4 = 0\;\] hoặc \[x + y - z - 8 = 0\;\].
B.\[x + y - z - 4 = 0\;\] hoặc \[x + y - z + 8 = 0\;.\]
C.\[x + y - z + 4 = 0\;\] hoặc \[x + y - z + 8 = 0\;\].
D.\[x + y - z - 4 = 0\;\] hoặc \[x + y - z - 8 = 0\;\].
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Vì (P) song song với (Q) nên\[\left( P \right):x + y - z + c = 0\]
Chọn A(2,0,0) thuộc (Q) ta có
\[d\left( {(P),(Q)} \right) = d\left( {A,(P)} \right) = \frac{{|2 + c|}}{{\sqrt 3 }} = 2\sqrt 3 \Leftrightarrow |2 + c| = 6\]
Suy ra c=4 hoặc c=−8.
Đáp án cần chọn là: A
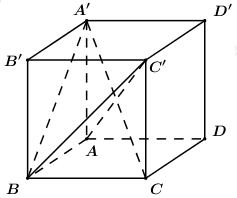
Cho hình lập phương ABCD.A′B′C′D′. Côsin góc giữa hai mặt phẳng (A′BC) và (ABC′) bằng:
Trong không gian Oxyz, cho ba điểm A(1,0,0),B(0,1,0) và C(0,0,1) . Phương trình mặt phẳng (P) đi qua ba điểm A,B,C là:
Viết phương trình mặt phẳng (P) đi qua điểm M(1;0;−2) và vuông góc với hai mặt phẳng (Q),(R) cho trước với \[\left( Q \right):x + 2y - 3z + 1 = 0\;\]và \[\left( R \right):2x - 3y + z + 1 = 0\;\].
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;1;2). Hỏi có bao nhiêu mặt phẳng (P) đi qua M và cắt các trục x′Ox,y′Oy,z′Oz lần lượt tại các điểm A,B,C sao cho \[OA = OB = OC \ne 0\]?
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(4,−1,2), B(2,−3,−2). Phương trình nào dưới đây là phương trình mặt phẳng trung trực của đoạn thẳng AB.
Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng qua điểm M(2,−3,4) và nhận \[\overrightarrow n = \left( { - 2,4,1} \right)\;\]làm vectơ pháp tuyến.
Cho mặt phẳng (P) có phương trình \[x + 3y - 2z + 1 = 0\;\] và mặt phẳng (Q) có phương trình \[x + y + 2z - 1 = 0\]. Trong các mặt phẳng tọa độ và mặt phẳng (Q) , xác định mặt phẳng tạo với (P) góc có số đo lớn nhất.
Trong không gian Oxyz, cho mặt phẳng \[\left( P \right):x - y + 3 = 0\]. Vec-tơ nào sau đây không là vecto pháp tuyến của mặt phẳng (P) .
Trong không gian với hệ tọa độ Oxyz, cho A(1,−3,2),B(1,0,1),C(2,3,0). Viết phương trình mặt phẳng (ABC) .
Trong không gian Oxyz, cho hai mặt phẳng \[\left( P \right):3x - my - z + 7 = 0,\left( Q \right):6x + 5y - 2z - 4 = 0.\] Hai mặt phẳng (P và (Q) song song với nhau khi m bằng
Cho hai điểm M(1;−2;−4),M′(5;−4;2). Biết M′ là hình chiếu của M lên mặt phẳng (P). Khi đó, phương trình (P) là:
Trong không gian với hệ trục Oxyz, mặt phẳng đi qua điểm A(1,3,−2) và song song với mặt phẳng \[(P):2x - y + 3z + 4 = 0\] là:
Trong không gian với hệ toạ độ Oxyz, cho hai mặt phẳng \[\left( P \right):x + 2y + 2z + 11 = 0\;\]và \[\left( Q \right):x + 2y + 2z + 2 = 0\;\]. Tính khoảng cách giữa (P) và (Q).
Cho hai mặt phẳng (P) và (Q) lần lượt có phương trình \[x + 2y - 2z + 1 = 0\;\] và \[x - 2y + 2z - 1 = 0\]. Gọi (S) là quỹ tích các điểm cách đều hai mặt phẳng (P) và (Q). Tìm khẳng định đúng.
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng \[\left( P \right):mx + y - 2z - 2 = 0\;\]và \[\left( Q \right):x - 3y + mz + 5 = 0\]. Tìm tất cả các giá trị thực của m để hai mặt phẳng đã cho vuông góc với nhau.