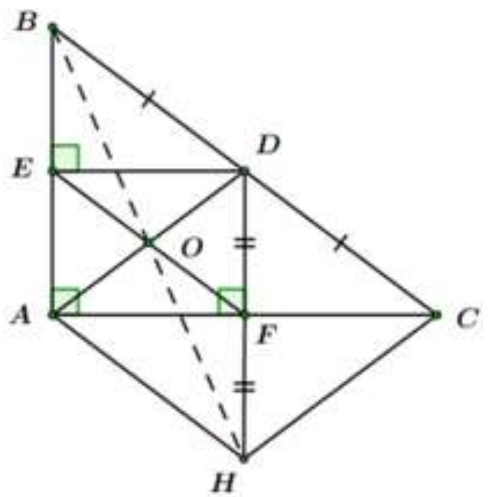
Cho tam giác ABC vuông tại , D là trung điểm của cạnh BC. Vẽ DE vuông góc với AB tại E, DF vuông góc với AC tại F.
Chứng minh rằng các đường thẳng đồng quy.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Phương pháp:
Cách giải:
Chứng minh rằng các đường thẳng AD, BH, EF đồng quy.
Gọi O là giao điểm của AD và EF.
là trung điểm của AD và EF.
Ta có tứ giác ADCH là hình thoi (cmt)
(tính chất hình thoi).
Mà .
Xét tứ giác ABDH ta có:
(cmt)
là hình bình hành. (dhnb)
cắt BH tại trung điểm của mỗi đường. (tính chất hbh).
Mà O là trung điểm của .
đồng quy tại O.
Thực hiện phép chia đa thức: cho đa thức .
Tìm giá trị nhỏ nhất của đa thức thương trong phép chia đa thức trên.
Cho tam giác ABC vuông tại , D là trung điểm của cạnh BC. Vẽ DE vuông góc với AB tại E, DF vuông góc với AC tại F.
Trên tia đối của tia FD lấy điểm H sao cho . Chứng minh rằng tứ giác ADCH là hình thoi.
Cho tam giác ABC vuông tại , D là trung điểm của cạnh BC. Vẽ DE vuông góc với AB tại E, DF vuông góc với AC tại F.
Chứng minh rằng tứ giác AEDF là hình chữ nhật và .
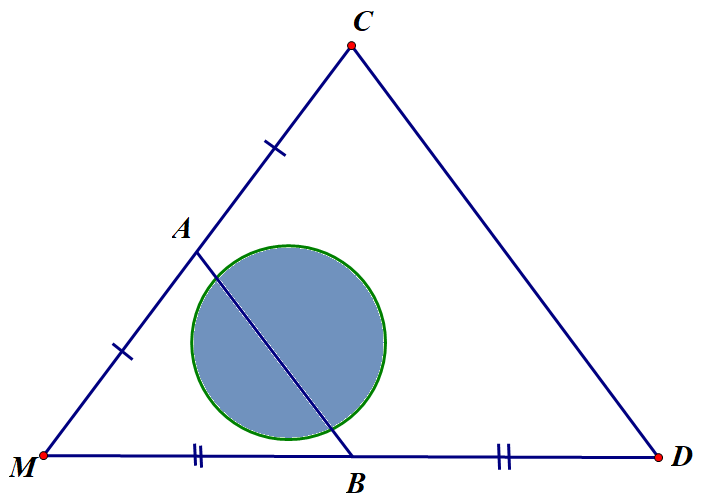
Giữa hai điểm A và B là một hồ nước sâu. Biết lần lượt là trung điểm của (xem hình vẽ). Bạn Mai đi từ C đến D với vận tốc 160m/phút hết 1 phút 30 giây. Hỏi hai điểm A và B cách nhau bao nhiêu mét?