Bộ 14 đề thi Học kì 1 Toán 8 có đáp án - Đề 7
-
2037 lượt thi
-
9 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Phân tích đa thức thành nhân tử:
Phương pháp:
Phân tích đa thức thành nhân tử nhờ các phương pháp đặt nhân tử chung, nhóm hạng tử chung hoặc phương pháp hằng đẳng thức.
Cách giải:
Câu 2:
Phân tích đa thức thành nhân tử:
Phương pháp:
Phân tích đa thức thành nhân tử nhờ các phương pháp đặt nhân tử chung, nhóm hạng tử chung hoặc phương pháp hằng đẳng thức.
Cách giải:
Câu 3:
Phương pháp:
Sử dụng các phương pháp phân tích đa thức thành nhân tử, quy đồng mẫu nhiều phân số
Cách giải:
Gọi số quả táo An mua là x, số quả lê An mua là y .
Theo bài ra ta có: Hiệu bình phương số quả táo và lê bằng 41 nên ta có:
(*)
Vì số quả táo nhiều hơn số quả lê nên và .
Vậy An đã mua 21 quả táo và 20 quả lê.
Câu 4:
Phương pháp:
Sử dụng các phương pháp phân tích đa thức thành nhân tử, quy đồng mẫu nhiều phân số
Cách giải:
Điều kiện:
.
Câu 5:
Thực hiện phép chia đa thức: cho đa thức .
Tìm giá trị nhỏ nhất của đa thức thương trong phép chia đa thức trên.
Phương pháp:
Biến đổi biểu thức, chia đa thức cho đa thức.
Sau đó biến đổi biểu thức thương tìm được về dạng: .
Dấu xảy ra .
Xét
Dấu xảy ra
Vậy khi .
Câu 6:
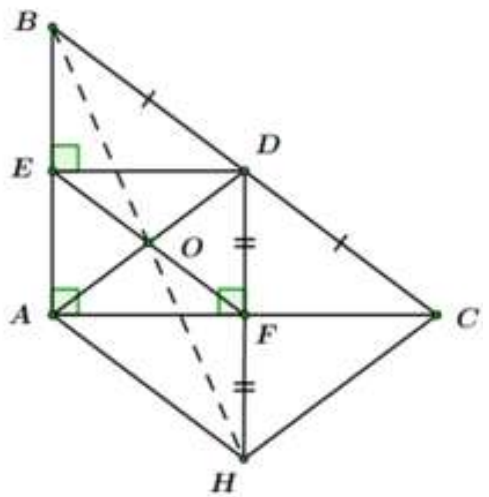
Cho tam giác ABC vuông tại , D là trung điểm của cạnh BC. Vẽ DE vuông góc với AB tại E, DF vuông góc với AC tại F.
Chứng minh rằng tứ giác AEDF là hình chữ nhật và .
Phương pháp:
Sử dụng dấu hiệu nhận biết hình chữ nhật và tính chất của nó.
Cách giải:
Chứng minh rằng tứ giác AEDF là hình chữ nhật và .
Xét tứ giác AEDF ta có:
(gt)
là hình chữ nhật. (dhnb)
(hai đường chéo hình chữ nhật).
Câu 7:
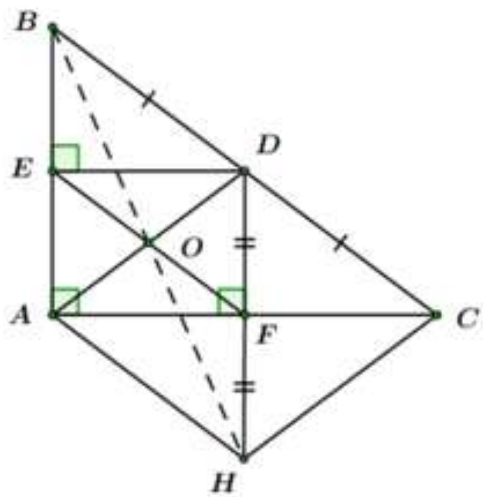
Cho tam giác ABC vuông tại , D là trung điểm của cạnh BC. Vẽ DE vuông góc với AB tại E, DF vuông góc với AC tại F.
Trên tia đối của tia FD lấy điểm H sao cho . Chứng minh rằng tứ giác ADCH là hình thoi.
Phương pháp:
Sử dụng dấu hiệu nhận biết hình thoi.
Cách giải:
Trên tia đối của tia FD lấy điểm H sao cho . Chứng minh rằng tứ giác ADCH là hình thoi.
Xét ta có:
D là trung điểm của BC (gt); (do AEDF là hình chữ nhật).
là trung điểm của AC.
Ta có: là trung điểm của DH.
Xét tứ giác ADCH ta có:
F là trung điểm của HD và AC.
là hình thoi. (dhnb).
Câu 8:
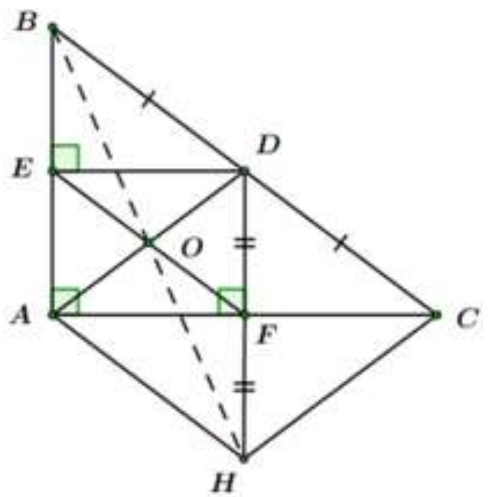
Cho tam giác ABC vuông tại , D là trung điểm của cạnh BC. Vẽ DE vuông góc với AB tại E, DF vuông góc với AC tại F.
Chứng minh rằng các đường thẳng đồng quy.
Phương pháp:
Cách giải:
Chứng minh rằng các đường thẳng AD, BH, EF đồng quy.
Gọi O là giao điểm của AD và EF.
là trung điểm của AD và EF.
Ta có tứ giác ADCH là hình thoi (cmt)
(tính chất hình thoi).
Mà .
Xét tứ giác ABDH ta có:
(cmt)
là hình bình hành. (dhnb)
cắt BH tại trung điểm của mỗi đường. (tính chất hbh).
Mà O là trung điểm của .
đồng quy tại O.
Câu 9:
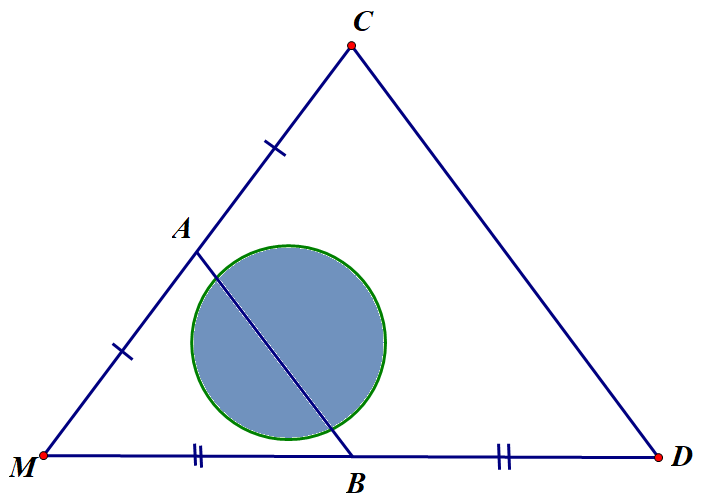
Giữa hai điểm A và B là một hồ nước sâu. Biết lần lượt là trung điểm của (xem hình vẽ). Bạn Mai đi từ C đến D với vận tốc 160m/phút hết 1 phút 30 giây. Hỏi hai điểm A và B cách nhau bao nhiêu mét?
Phương pháp:
Dựa vào tính chất đường trung bình của tam giác.
Cách giải:
Đổi 1 phút 30 giây phút.
Xét ta có:
A là trung điểm MC (gt)
B là trung điểm MD (gt)
là đường trung bình của (định lý).
(tính chất đường trung bình của tam giác).
Quãng đường bạn Mai đã đi là:
Vậy hai điểm A và B cách nhau .
