Cho tam giác ABC cân tại A có đường cao AH (H thuộc BC). Gọi M là trung điểm của đoạn thẳng AB. Gọi E là điểm đối xứng với H qua M
Chứng minh tứ giác AHBE là hình chữ nhật.
Giải bởi qa.haylamdo.com
Phương pháp:
Sử dụng dấu hiệu nhận biết: “Tứ giác có hai đường chéo giao nhau tại trung điểm mỗi đường là hình bình hành” và “Hình bình hành có 1 góc vuông là hình chữ nhật”
Cách giải:
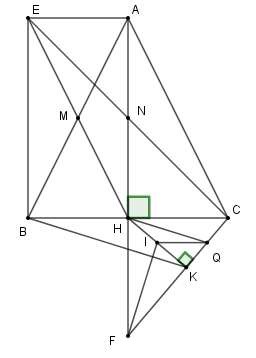
Xét tứ giác AHBE có
M là trung điểm AB (giả thiết)
M là trung điểm EH (E đối xứng với H qua M)
Tứ giác AHBE là hình bình hành (dấu hiệu nhận biết hình bình hành).
Mà
AHBE là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật).
Cho hai biểu thức: và với
Cho P= A.B. Tìm giá trị nguyên của x để P có giá trị nguyên.
Cho tam giác ABC cân tại A có đường cao AH (H thuộc BC). Gọi M là trung điểm của đoạn thẳng AB. Gọi E là điểm đối xứng với H qua M.
Gọi N là trung điểm của AH. Chứng minh N là trung điểm của EC.
Cho tam giác ABC cân tại A có đường cao AH (H thuộc BC). Gọi M là trung điểm của đoạn thẳng AB. Gọi E là điểm đối xứng với H qua M.
Cho . Tính diện tích tam giác AMH.
Cho tam giác ABC cân tại A có đường cao AH (H thuộc BC). Gọi M là trung điểm của đoạn thẳng AB. Gọi E là điểm đối xứng với H qua M.
Trên tia đối của tia HA lấy điểm F. Kẻ (K thuộc FC). Gọi I, Q lần lượt là trung điểm của HK, KC. Chứng minh rằng: .
