Câu hỏi:

19/10/2022 120

Cho tam giác ABC cân tại A có AH là đường cao và D là trung điểm của cạnh AC. Gọi E là điểm đối xứng của H qua điểm D

a) Chứng minh tứ giác AHCE là hình chữ nhật

b) Chứng minh HE = AB

c) Gọi G là giao điểm của BD và AH. Đường thẳng CG cắt AB tại F. Chứng minh EF song song với BG.

Xem lời giải

Bắt Đầu Thi Thử

Trả lời:

Giải bởi qa.haylamdo.com

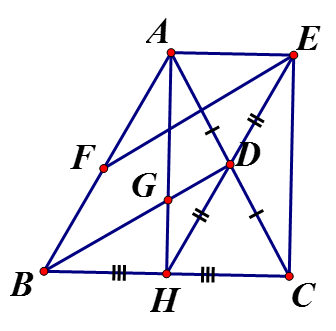
a) Ta có: $\{\begin{cases} AD = DC \\ HD = HE \end{cases} \Rightarrow AECH$ là hình bình hành

Mà $ΔABC$ cân tại $A \Rightarrow AH$ là đường cao $\Rightarrow \hat{AHC} = 90^{0} \Rightarrow AECH$ là hình chữ nhật

b) Ta có AECH là hình chữ nhật $\Rightarrow EH = AC$ mà $AB = AC (ΔABC$ cân)

$\Rightarrow EH = AB$

c) Ta có: $ΔABC$ cân nên AH đường cao cũng là trung tuyến $\Rightarrow BH = HC$

Mà $HC = AE$ (tính chất hình chữ nhật) $\Rightarrow BH = AE$ mà BH//AE nên

$AEHB$ là hình bình hành $\Rightarrow AB = HE$ và AB = HE
$\Rightarrow \frac{1}{2} AB = \frac{1}{2} HE \Rightarrow \{\begin{cases} FB = DE \\ FB / / DE \end{cases} \Rightarrow FEDB$ là hình bình hành $\Rightarrow EF / / BD \Rightarrow EF / / BG$

Câu trả lời này có hữu ích không?

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Diện tích hình chữ nhật sẽ thay đổi như thế nào khi tăng chiều rộng lên 3 lần và giữ nguyên chiều dài ?

Xem đáp án » 19/10/2022 152

Câu 2:

Thực hiện phép tính 2x(x+5) được kết quả là

Xem đáp án » 19/10/2022 132

Câu 3:

Tứ giác ABCD là hình bình hành. Cần thêm điều kiện gì về hai đường chéo để ABCD là hình chữ nhật

Xem đáp án » 19/10/2022 116

Câu 4:

Thực hiện phép chia $(4 x^{2} y^{3} - 6 x^{3} y^{2}) : (2 {xy}^{2})$ được kết quả là

Xem đáp án » 19/10/2022 100

Câu 5:

Thực hiện phép chia $(x^{2} - 5 x + 6) : (x - 3)$ được thương là:

Xem đáp án » 19/10/2022 91

Câu 6:

Trong đẳng thức $a^{3} - b^{3} = (a - b) (.....)$ , biểu thức còn thiếu tại “…..” là

Xem đáp án » 19/10/2022 90

Câu 7:

Phân thức đối của phân thức $\frac{x + 1}{x}$ là

Xem đáp án » 19/10/2022 89

Câu 8:

Khai triển biểu thức ${(x - 1)}^{2}$ được kết quả là

Xem đáp án » 19/10/2022 87

Câu 9:

Thực hiện phép chia $10 x^{2} y^{4} : (5 xy)$ được kết quả là

Xem đáp án » 19/10/2022 83

Câu 10:

Phân tích các đa thức sau thành nhân tử: $x^{2} - 4 y^{2} + 2 x + 1$

Xem đáp án » 19/10/2022 78

Câu 11:

Tứ giác ABCD có số đo các góc là: $A = 70^{0}; B = 80^{0}; C = 90^{0}$ . Số đo góc D bằng

Xem đáp án » 19/10/2022 75

Câu 12:

Hình nào sau đây là một đa giác đều

Xem đáp án » 19/10/2022 72

Câu 13:

Phân tích các đa thức sau thành nhân tử: $3 x^{2} - 3 xy$

Xem đáp án » 19/10/2022 70

Câu 14:

Hai phân thức $\frac{C}{D}$ và $\frac{E}{F}$ bằng nhau khi nào ?

Xem đáp án » 19/10/2022 69

Câu 15:

Thực hiện các phép tính sau: $\frac{2 x - 3}{7} + \frac{5 x + 3}{7}$

Xem đáp án » 19/10/2022 69

Xem thêm các câu hỏi khác »

Đề thi liên quan

Xem thêm »

Trắc nghiệm Toán 8 Nhân đơn thức với đa thức, đa thức với đa thức có lời giải chi tiết

2 đề 9017 lượt thi Thi thử
Bài tập Nhân đơn thức với đa thức (có lời giải chi tiết)

2 đề 5909 lượt thi Thi thử
Top 12 Đề kiểm tra Toán 8 Học Kì 2 Chương 3 Đại Số có đáp án, cực hay

16 đề 4540 lượt thi Thi thử
Tổng hợp bài tập Toán 8 Chương 3: Phương trình bậc nhất một ẩn

13 đề 4533 lượt thi Thi thử
Bài tập Những hằng đẳng thức đáng nhớ (có lời giải chi tiết)

2 đề 3562 lượt thi Thi thử
Top 8 Đề kiểm tra Toán 8 Học Kì 1 Chương 1 Hình học có đáp án, cực hay

9 đề 3285 lượt thi Thi thử
Đề thi Toán lớp 8 Giữa học kì 2 năm 2020 - 2021 có đáp án

10 đề 3113 lượt thi Thi thử
Bài tập Nhân đa thức với đa thức (có lời giải chi tiết)

2 đề 2546 lượt thi Thi thử
Top 11 Đề kiểm tra Đại số Toán 8 Học Kì 1 Chương 1 có đáp án, cực hay

6 đề 2513 lượt thi Thi thử
Top 8 Đề kiểm tra Đại Số Toán 8 Học Kì 1 Chương 2 có đáp án, cực hay

9 đề 2481 lượt thi Thi thử

Xem thêm »

Hỏi bài

Câu hỏi mới nhất

Xem thêm »

3) Tính số đo các góc của $Δ D M N$ .

128 19/10/2022 Xem đáp án
2) Chứng minh: $Δ A M D = Δ B N D$ .

130 19/10/2022 Xem đáp án
Cho hình thoi ABCD có AB = BD. Gọi M, N lần lượt trên các cạnh AB, BC sao cho AM + NC = AD.

1) Chứng minh: AM = BN.

162 19/10/2022 Xem đáp án
3) Tổng độ dài (DM + DN) không đổi.

101 19/10/2022 Xem đáp án
2) $Δ A B M = Δ D B N$

106 19/10/2022 Xem đáp án
Cho hình thoi ABCD có $\hat{A} = 60 °$ . Một góc xBy thay đổi sao cho tia Bx cắt cạnh AD tại M, tia By cắt cạnh CD tại N và $\hat{x B y} = 60 °$ . Chứng minh :

1) AB = BD.

157 19/10/2022 Xem đáp án
4) Tính diện tích hình thoi ABCD.

106 19/10/2022 Xem đáp án
3) Biết chu vi của hình thoi ABCD là 8cm . Tính độ dài đường chéo BD ; AC.

103 19/10/2022 Xem đáp án
2) Gọi O là giao điểm của AC và BD. Chứng minh: $O A^{2} = \frac{3}{4} A B^{2}$ .

104 19/10/2022 Xem đáp án
Cho hình thoi ABCD có AB = BD.

1) Chứng minh: Tam giác ABD đều.

104 19/10/2022 Xem đáp án

Xem thêm »

CHỌN BỘ SÁCH BẠN MUỐN XEM

Câu hỏi:

Trả lời:

Câu trả lời này có hữu ích không?

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Diện tích hình chữ nhật sẽ thay đổi như thế nào khi tăng chiều rộng lên 3 lần và giữ nguyên chiều dài ?

Câu 2:

Thực hiện phép tính 2x(x+5) được kết quả là

Câu 3:

Tứ giác ABCD là hình bình hành. Cần thêm điều kiện gì về hai đường chéo để ABCD là hình chữ nhật

Câu 4:

Thực hiện phép chia 4x2y3−6x3y2:2xy2 được kết quả là

Câu 5:

Thực hiện phép chia x2−5x+6:x−3 được thương là:

Câu 6:

Trong đẳng thức a3−b3=a−b..... , biểu thức còn thiếu tại “…..” là

Câu 7:

Thực hiện phép chia $(4 x^{2} y^{3} - 6 x^{3} y^{2}) : (2 {xy}^{2})$ được kết quả là

Thực hiện phép chia $(x^{2} - 5 x + 6) : (x - 3)$ được thương là:

Trong đẳng thức $a^{3} - b^{3} = (a - b) (.....)$ , biểu thức còn thiếu tại “…..” là