Cho a3 + b3 + c3 = 3abc và a + b + c ≠ 0. Tính giá trị của biểu thức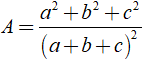 
Giải bởi qa.haylamdo.com
Ta có: a3 + b3 + c3 = 3abc ⇔ a3 + b3 + c3 - 3abc = 0
⇔ ( a + b )3 + c3 - 3ab( a + b ) - 3abc = 0
⇔ ( a + b )3 + c3 - 3ab( a + b + c ) = 0
⇔ ( a + b + c )3 - 3( a + b )c( a + b + c ) - 3ab( a + b + c ) = 0
⇔ ( a + b + c )( a2 + b2 + c2 - ab - bc - ca ) = 0
⇒ a2 + b2 + c2 - ab - bc - ca = 0 (vì a + b + c ≠ 0. )
⇔ a2 + b2 + c2 = ab + bc + ca.
Khi đó ta có:
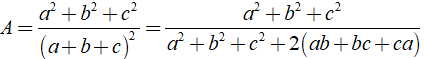
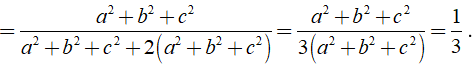
Vậy A= 1/3
