Cho a + b = 1. Tính giá trị của các biểu thức sau:

M = a³ + b³ + 3ab(a² + b²) + 6a²b²(a + b).

Cho tam giác ABC vuông tại A (AB < AC).Gọi I là trung điểm của cạnh BC. Qua I vẽ IM vuông góc với AB tại M và IN vuông góc với AC tại N.

a) Chứng minh tứ giác AMIN là hình chữ nhật.

b) Gọi D là điểm đối xứng của I qua N. Chứng minh tứ giác ACID là hình thoi.

c) Cho AC = 20cm, BC = 25cm.Tính diện tích ΔABC

d) Đường thẳng BN cắt cạnh DC tại K. Chứng minh:

Cho biểu thức

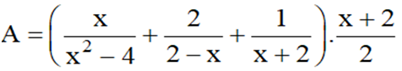
a) Tìm điều kiện của x để biểu thức A xác định.

b) Rút gọn A

c) Tính giá trị của A khi x= -1

Khẳng định nào sau đây là sai:                    

Gía trị của x thỏa mãn x² + 16 = 8x là

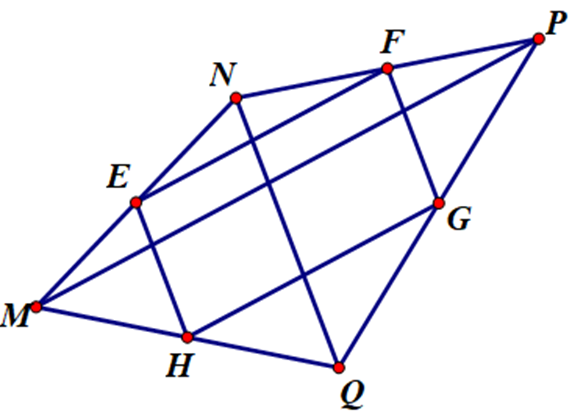
Cho tứ giác MNPQ. Gọi E, F , G, H lần lượt là trung điểm các cạnh MN, NP, PQ, QM. Tứ giác EFGH là hình thoi nếu 2 đường chéo MP, NQ của tứ giác MNPQ:

Kết quả phân tích đa thức -x² + 4x - 4 là:

Kết quả phép tính: 15 x³y⁵z : 3 xy²z là

Mẫu thức chung của 2 phân thức:

Điều kiện xác định của phân thức: 

Phân tích thành nhân tử:

Độ dài 2 đường chéo của hình thoi lần lượt là 6 cm và 4 cm. Độ dài cạnh của hình thoi là:

Phân tích thành nhân tử: