Cho hình thang cân ABCD (AB // CD, AB < CD ). Kẻ các đường cao AE, BF của hình thang. Chứng minh rằng DE = CF.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
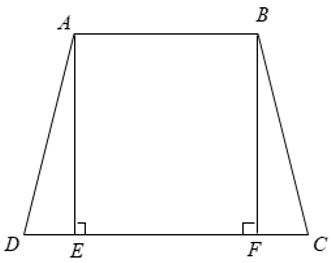
Ta có ABCD là hình thang cân nên AD = BC
+ Xét tam giác vuông ADE có
AD2 = AE2 + DE2 ⇒ DE2 = AD2 - AE2 ⇔ DE = √( AD2 - AE2 ) ( 1 )
+ Xét tam giác vuông BCF có:
BC2 = BF2 + CF2 ⇒ CF2 = BC2 - BF2 ⇔ CF = √( BC2 - BF2 ) ( 2 )
Mà ABCD là hình thang cân nên AE = BF ( 3 )
Từ ( 1 ), ( 2 ) và ( 3 ) ⇒ DE = CF (do AD = BC và AE = BF )
Cho hình thang cân ABCD ( AB//CD,AB < CD ). Kẻ đường cao AH,BK của hình thang. Chứng minh rằng DH = CK.
Điền cụm từ thích hợp vào chỗ trống
Hình thang cân là…………………………………..
Điền chữ “Đ” hoặc “S” vào mỗi câu khẳng định sau:
Tứ giác có hai cạnh bên bằng nhau là hình thang cân.