Cho hình thang ABCD có đáy AB và CD, biết AB = 4cm, CD = 8cm, BC = 5cm, AD = 3cm. Chứng minh: ABCD là hình thang vuông.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
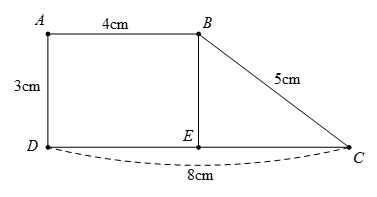
Qua B, kẻ BE // AD
Hình thang ABCD có đáy AB và CD
=> AB // CD
=> AB // DE
=> ABED là hình thang
Mà BE // AD
(theo tính chất hình thang có hai cạnh bên song song)
Mà
=>
Có
=>
Có vuông tại E (theo định lý Pytago đảo)
=>
Mà
=>
Mà ABCD là hình thang
=> ABCD là hình thang vuông
Cho hình thang ABCD (AB // CD)
a) Phân giác của và cắt nhau tại điểm I trên cạnh BC. Chứng minh: AD = AB + CD.
Cho hình thang ABCD (AB // CD) có M là trung điểm của BC và . Chứng minh: DM là phân giác của .
Cho tứ giác ABCD có và góc ngoài tại đỉnh A là .
a) Tứ giác ABCD là hình gì? Vì sao?
Cho hình thang ABCD (AB // CD). Biết AB < CD, AD < BC. Chứng minh :
a) AD + BC > CD - AB.
Cho vuông cân tại A. Ở phía ngoài vẽ vuông cân tại B. Chứng minh tứ giác ABDC là hình thang.