Cho tam giác ABC có . Tia phân giác của góc ngoài tại A cắt đường thẳng BC ở E. Tính độ dài EB.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
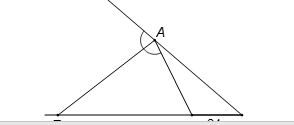
Áp dụng tính chất của đường phân giác ngoài AE vào tam giác ABC, ta được:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
Vậy .