Cho tam giác ABC với đường trung tuyến AM và phân giác AD. Tính diện tích tam giác ABC biết AB=m,AC=n (n>m).
Giải bởi qa.haylamdo.com
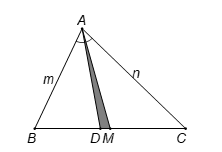
Ta có SADMSABC=DMBC hay SADM=DMBC.S
(vì chung chiều cao kẻ từ A đến BC, với S=SABC).
Ta còn phải tính tỉ số DM:BC.
Áp dụng tính chất của đường phân giác AD vào tam giác ABC,
ta được:
DBDC=BACA=mn⇒{DB=mtDC=nt (với t>0).
Do đó BC=DB+DC=(m+n).t, nên: BM=12BC=(m+n)t2.
⇒DM=BM−BD=(m+n)t−mt2=(n−m)t2.
Suy ra tỉ số DM:BC=(n−m)t2:(m+n)t=n−m2(m+n).
Vậy SADM=n−m2(m+n).S.
Cho n=7cm,m=3cm. Hỏi diện tích tam giác ADM chiếm bao nhiêu phần trăm diện tích tam giác ABC?
Cho tam giác ABC với đường trung tuyến AM. Tia phân giác của góc AMB cắt cạnh AB ở D, tia phân giác của góc AMC cắt các cạnh AC ở E. Chứng minh rằng DE∥BC.
