Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
c) Ta có
(đáy lớn gấp đôi đáy nhỏ)
Cho tứ giác ABCD. Gọi M và N lần lượt là trung điểm của AB và CD. Gọi G là trọng tâm của tam giác BCD. Chứng minh AG chia đôi MN.
Cho tam giác ABC, BC = 6 cm. Trên cạnh AB lấy điểm D sao cho . Vẽ . Tính độ dài DE.
Cho tam giác ABC, trung tuyến AM. Gọi I là trung điểm của AM, D là giao điểm của BI và AC
a) Chứng minh:
Tính độ dài đường trung bình của một hình thang cân biết rằng các đường chéo của nó vuông góc với nhau và đường cao bằng 10cm .
Cho tam giác ABC, AM là trung tuyến. Vẽ đường thẳng d qua trung điểm I của AM cắt các cạnh AB, AC. Gọi A', B' ,C' thứ tự là hình chiếu của A, B, C lên đường thẳng d . Chứng minh rằng BB' + CC' = AA' .
Cho tam giác nhọn ABC. Gọi M, N lần lượt là trung điểm của AB, AC. Chứng minh rằng tứ giác BMNC là hình thang.
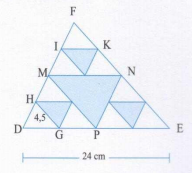
Trong hình sau, mỗi cạnh của tam giác màu xanh là đường trung bình tương ứng của các cạnh tam giác màu trắng. Hãy tính IK, EF.
Cho tứ giác ABCD có chụ vi là 4a. Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh rằng trong hai đoạn thẳng EG và HF có một đoạn thẳng có độ dài không lớn hơn a.
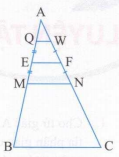
Ở hình sau, cho biết MN là đường trung bình của tam giác ABC, EF là đường trung bình của hình thang QWNM. Biết BC = 20 cm, EF = 3x, QW = x. Tính x.