Cho điểm M nằm trên đoạn thẳng AB, Vẽ về một phía của AB các tia Ax, By vuông góc với AB. Lấy điểm C thuộc tia Ax, điểm D thuộc tia By sao cho Chứng minh rằng: .
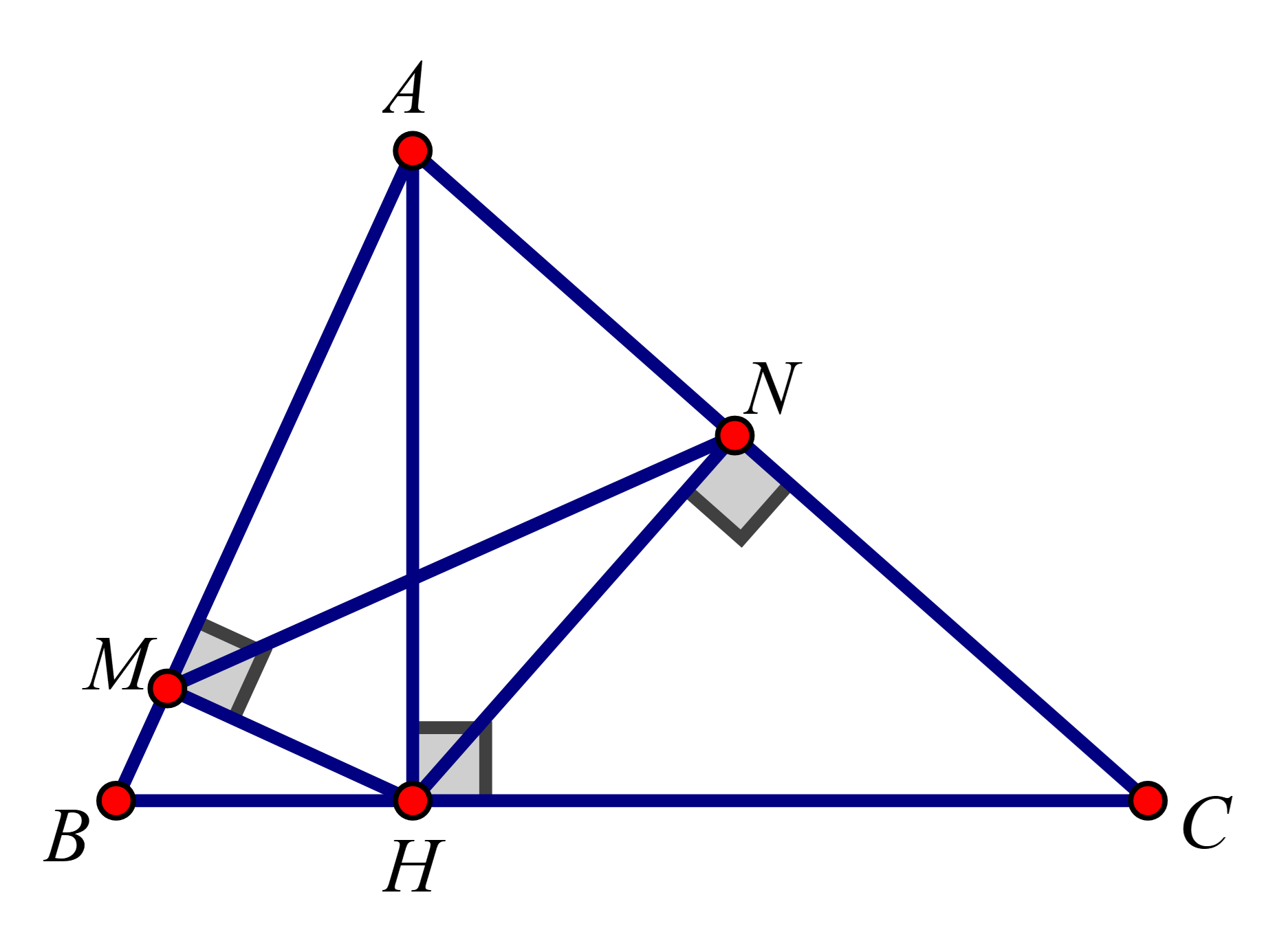
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
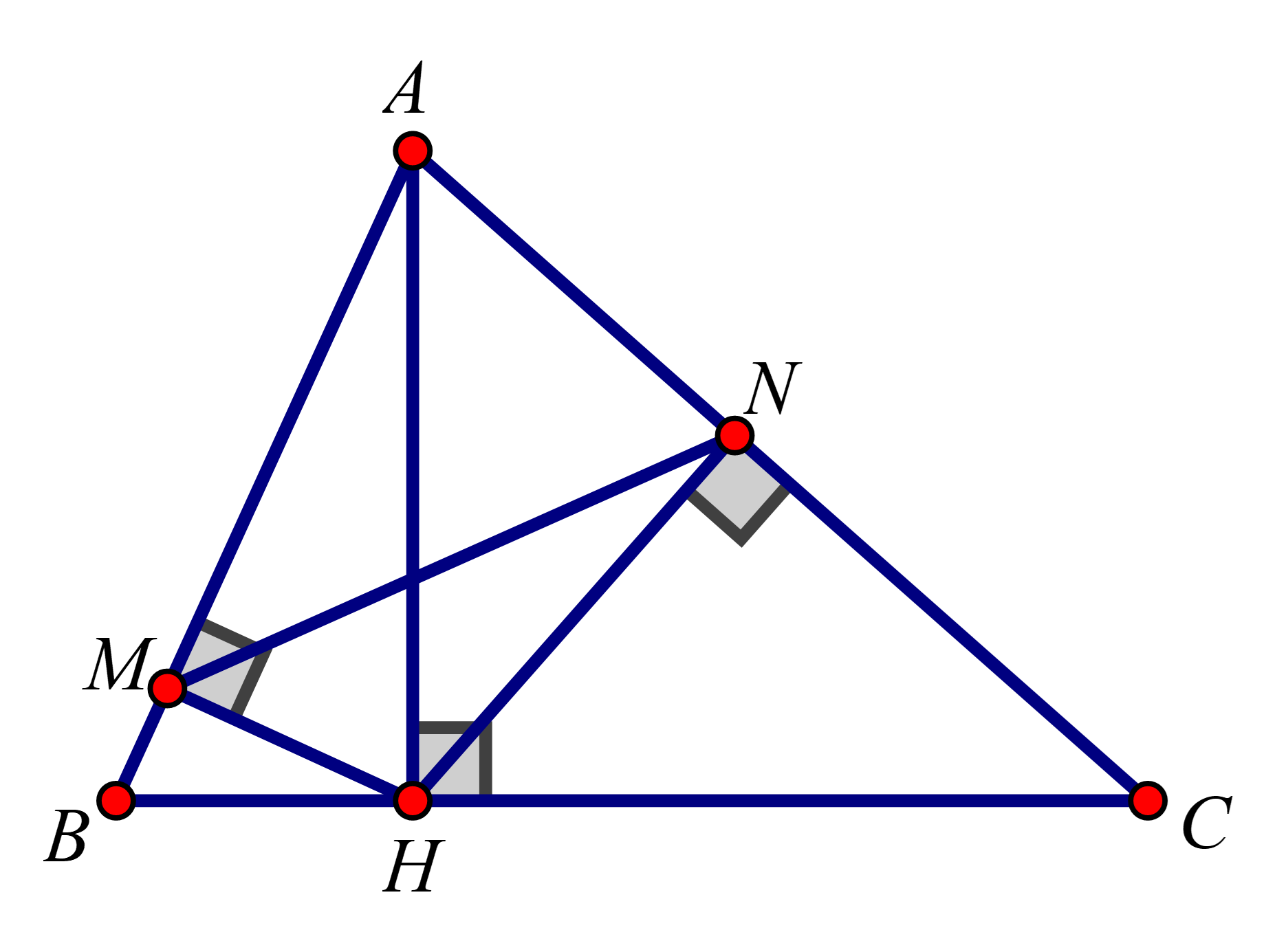
Ta tính được BD = 18 cm.
Xét tam giác AMC và BDM:
Suy ra: mà
Nên và
Vậy
Tam giác ABH vuông tại H có Trên tia đối của tia HB lấy điểm C sao cho Tính
Cho tam giác ABC vuông tại A, Ở phía ngoài tam giác ABC, vẽ tam giác BCD vuông tại C có BD = 9cm. Chứng minh rằng .
Tam giác ABH vuông tại H có Trên tia đối của tia HB lấy điểm C sao cho