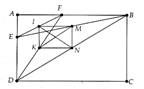
Cho hình chữ nhật ABCD. Điểm E thuộc cạnh AD, điểm F thuộc cạnh AB. Gọi I, K, M, N theo thứ tự là trung điểm của EF, FD, BE, BD. Chứng minh IN = KM.

Cho tam giác ABC vuông cân tại C. Trên các cạnh AC, BC lấy lần lượt các điểm P, Q sao cho AP = CQ. Từ điểm P vẽ PM song song với BC (M $\in$ AB). Chứng minh tứ giác PCQM là hình chữ nhật.

Cho tam giác ABC vuông tại A. Về phía ngoài tam giác ABC, vẽ hai tam giác vuông cân ADB (DA = DB) và ACE (EA = EC). Gọi M là trung điểm của BC, I là giao điểm của DM với AB, và K là giao điểm của EM với AC. Chứng minh:

a) Ba điểm D, A, E thẳng hàng.

Cho tam giác ABC vuông tại A, đường cao AH. Gọi I, K theo thứ tự là trung điểm của AB, AC. Chứng minh:

a) $\widehat{IHK}={90}^0.$ 

Cho hình thang vuông ABCD ($\widehat{A}=\widehat{D}={90}^0$) có các điểm E và F thuộc cạnh AD sao cho AE = DF và $\widehat{BFC}={90}^0$. Chứng minh $\widehat{BEC}={90}^0.$ 

c) Tam giác DME là tam giác vuông cân.

b) AF song song với BD;

b) Xác định vị trí của điểm O để tứ giác MNPQ là hình chữ nhật.

c) Ba điểm E, H, K thẳng hàng.

Cho tam giác ABC có đường cao AI. Từ A kẻ tia Ax vuông góc với AC, từ B kẻ tia By song song với AC. Gọi M là giao điểm của tia Ax và tia By. Nối M với trung điểm P của AB, đường MP cắt AC tại Q và BQ cắt AI tại H.

a) Tứ giác AMBQ là hình gì ?

b) Chứng minh rằng CH $\perp$AB.

b) Tứ giác IAKM là hình chữ nhật.

b) Chu vi $△$IHK bằng nửa chu vi $△$ABC.

Cho tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H theo thứ tự là trung điẻm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì ?

c) Chứng minh tam giác PIQ cân.

b) Chứng minh HG = GK = KE.