Đề thi Giữa kì 1 Vật lí 9 có đáp án (Đề 2)
-
1669 lượt thi
-
16 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Biểu thức của định luật Ôm:\[I = \frac{U}{R} \Rightarrow \left\{ \begin{array}{l}I \sim U\\I \sim \frac{1}{R}\end{array} \right.\]
Cường độ dòng điện chạy qua dây dẫn càng lớn thì điện trở của dây dẫn càng nhỏ.
Chọn đáp án A
Câu 2:
Công thức tính điện trở của một dây dẫn: \[R = \rho \frac{\ell }{S}\]
Chọn đáp án B
Câu 3:
Một dây nhôm dài 100m, có tiết diện 1mm2thì có điện trở là 1,7\[\Omega \]. Một dây nhôm khác có tiết diện 0,2mm2có điện trở là 17\[\Omega \] thì có chiều dài là:
Tóm tắt:
\[{\ell _1}\] = 100 m
S1= 1 (mm2)
\[{R_1} = 1,7\Omega \]
\[{S_2} = 0,2\left( {m{m^2}} \right)\]
\[{R_2} = 17\Omega \]
\[{\ell _2} = ?\]
Giải:
Công thức tính điện trở của một dây dẫn: \[R = \rho \frac{\ell }{S}\]
Lập tỉ số: \[\frac{{{R_1}}}{{{R_2}}} = \frac{{{\ell _1}}}{{{\ell _2}}}.\frac{{{S_2}}}{{{S_1}}} \Leftrightarrow \frac{{1,7}}{{17}} = \frac{{100}}{{{\ell _2}}}.\frac{{0,2}}{1} \Rightarrow {\ell _2} = 200m\]
Chọn đáp án C
Câu 4:
Dây dẫn được làm từ cùng loại vật liệu, nếu gập đôi dây dẫn thì điện trở của dây dẫn:
Công thức tính điện trở của một dây dẫn: \[R = \rho \frac{\ell }{S} \Rightarrow \left\{ \begin{array}{l}R \sim \ell \\R \sim \frac{1}{S}\end{array} \right.\]
Nếu gập đôi chiều dài dây dẫn thì \[\ell = \frac{{{\ell _o}}}{2}\] và \[S = 2{S_0}\] (\[{\ell _o}\]và S0là chiều dài và tiết diện của dây dẫn ban đầu) Điện trở của dây dẫn giảm đi 4 lần.
Chọn đáp án B
Câu 5:
Một dây nikêlin tiết diện đều có điện trở 55Ω dài 5,5m. Tính tiết diện của dây nikêlin. Biết điện trở suất của nikêlin là 0,4.10-6Ωm
Tómtắt:
\[R = 55{\rm{ }}\Omega \]
\[\ell = 5,5m\]
\[\rho = 0,{4.10^{ - 6}}\Omega .m\]
S = ?
Giải:
Tiết diện của dây dẫn: \[S = \rho \frac{\ell }{R} = 0,{4.10^{ - 6}}.\frac{{5,5}}{{55}} = 0,{04.10^{ - 6}}{m^2} = 0,04{\rm{ }}m{m^2}\]
Chọn đáp án D
Câu 6:
Cho đoạn mạch gồm 3 điện trở:R1= R2= R3= 60 mắc song song với nhau. Rtđcủa đoạn mạch có giá trị nào trong các giá trị sau:
Ta có: R1//R2//R3
Điện trở tương đương của đoạn mạch là:
\[\frac{1}{{{R_{td}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} + \frac{1}{{{R_3}}} = \frac{1}{{60}} + \frac{1}{{60}} + \frac{1}{{60}} = \frac{1}{{20}}\]
\[ \Rightarrow {R_{td}} = 20\Omega \]
Chọn đáp án A
Câu 7:
Cho đoạn mạch gồm 3 điện trở R1= R2= R3= 12\(\Omega \) mắc nối tiếp. Điện trở tương đương của đoạn mạch có giá trị nào trong các giá trị sau:
Ta có: R1 nt R2 nt R3
Điện trở tương đương của đoạn mạch là:
\[{R_{td}} = {R_1} + {R_2} + {R_3} = 12 + 12 + 12 = 36\Omega \]
\[ \Rightarrow {R_{td}} = 36\Omega \]
Chọn đáp án B
Câu 8:
Biểu thức của định luật Ôm:\[I = \frac{U}{R}\]
Chọn đáp án B
Câu 9:
Mạch điện kín gồm hai bóng đèn được mắc nối tiếp, khi một trong hai bóng đèn bị hỏng thì mạch hở nên bóng đèn còn lại sẽ không hoạt động.
Chọn đáp án C
Câu 10:
+ Khi Uđ= Uđmđèn sáng bình thường.
+ Khi Uđ< Uđm
đèn sáng yếu hơn bình thường.+ Khi Uđ>Uđmđèn sáng mạnh hơn bình thường.
Chọn đáp án B
Câu 11:
Điện năng tiêu thụ trong 1 tháng (30 ngày) là
A = P.t = 20.5.30 = 3000 Wh = 3 kWh.
Chọn đáp án B
Câu 12:
Công suất tiêu thụ của bóng đèn là
P = U.I = 6.500.10-3= 3 W
Chọn đáp án D
Câu 13:
- Phát biểu nội dung định luật Ôm: Cường độ dòng điện chạy qua dây dẫn tỉ lệ thuận với hiệu điện thế đặt vào hai đầu đoạn dây và tỉ lệ nghịch với điện trở của dây.
- Biểu thức của định luật Ôm: \[I = \frac{{\rm{U}}}{{\rm{R}}}\]
Trong đó:
+ I là cường độ dòng điện chạy qua dây dẫn, đo bằng Ampe (A).
+ U là hiệu điện thế đặt vào hai đầu đoạn dây, đo bằng Vôn (V).
+ R là điện trở của dây, đo bằng Ôm (Ω).
Câu 14:
Một bóng đèn có ghi 12V – 9W. Cho biết ý nghĩa của con số ghi trên đèn và phải mắc bóng đèn vào hiệu điện thế bằng bao nhiêu để nó hoạt động bình thường?
- Ý nghĩa con số 12V – 9W: Khi hiệu điện thế định mức của đèn là 12V thì công suất định mức của đèn là 9W.
- Để đèn hoạt động bình thường thì phải mắc bóng đèn vào hiệu điện thế 12V.
Câu 15:
a) Tính công suất của bếp điện.
b) Tính điện năng mà bếp tiêu thụ trong khoảng thời gian trên ra đơn vị Jun và số đếm của công tơ điện.
Tóm tắt:
R = 48,5Ω
U = 220 V
t = 15 phút
a. P = ?
b. A = ? J = ? kWh (số điện)
Giải:
a. Công suất của bếp:
P = \(\frac{{{U^2}}}{R} = \frac{{{{220}^2}}}{{48,5}} \approx 998\left( {\rm{W}} \right)\)
b. Điện năng mà bếp tiêu thụ: A = P .t = 998.(15.60) = 898200 (J)
Số đếm của công tơ điện: \[A = \frac{{898200}}{{3600000}} = 0,2495{\rm{ kWh}} = 0,2495\]số điện.
Câu 16:
Cho mạch điện như hình vẽ hiệu điện thế giữa hai đầu đoạn mạch là 24V. Biến trở được làm bằng chất có điện trở suất 0,5.10-6\[\Omega \]m, dài 6m và tiết diện là 0,2 mm2
Trên đèn Đ có ghi 20V – 0,8A, điện trở R = 12\[\Omega \].
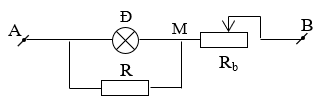
a) Tính giá trị lớn nhất của biến trở.
b) Khi biến trở có điện trở lớn nhất, tính điện trở tương đương của mạch
và để đèn sáng bình thường ta phải điều chỉnh biến trở, tính giá trị điện trở
của biến trở lúc này.
Tóm tắt:
U = 24 V
\[\rho = 0,{5.10^{ - 6}}\Omega .m\]
\[\ell = 6m\]
S = 0,2 mm2= 0,2.10-6m2
Đ: 20V – 0,8A
R = 12Ω
a. Rmax bt = ?
b. Rtđ= ?, Rb= ?
Giải:
a. Điện trở lớn nhất của biến trở:
\({R_{max\,bt}} = \rho \frac{\ell }{S} = 0,{5.10^{ - 6}}\frac{6}{{0,{{2.10}^{ - 6}}}} = 15\left( \Omega \right)\)
b.
+ Mạch điện gồm (Rđ//R) nt Rb
\[{R_d} = \frac{{U_d^2}}{{{{\rm{P}}_d}}} = \frac{{{{20}^2}}}{{16}} = 25\left( \Omega \right)\]
\[{R_{AM}} = \frac{{{R_d}R}}{{{R_d} + R}} = \frac{{25.12}}{{25 + 12}} \approx 8,1\Omega \]
Rtđ= RAM+ Rtp= 8,1 + 15 = 23,1 (\[\Omega \])
+ Để đèn sáng bình thường thì: Iđ= 0,8 (A) và IR= \[\frac{{{U_d}}}{R} = \frac{{20}}{{12}} = \frac{5}{3}\](A)
⇒ Ib= Iđ+ IR= 0,8 + \[\frac{5}{3}\] 2,5 (A)
Vậy điện trở của bếp là:
\[{R_b} = \frac{{U - {U_d}}}{{{I_b}}} = \frac{{24 - 20}}{{2,5}} = 1,6\left( \Omega \right)\]
