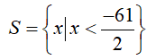Giải các bất phương trình và biểu diễn nghiệm trên trục số:
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
a)
⇔ x2 + 6x + 9 – 10 ≥ x2 + 3x + 2x + 6 – 4
⇔ x2 – x2 + 6x – 3x – 2x ≥ –9 + 10 + 6 – 4
⇔ x ≥ 3
Tập nghiệm: S = {x | x ≥ 3}.
Biểu diễn trên trục số:
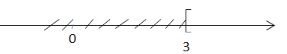
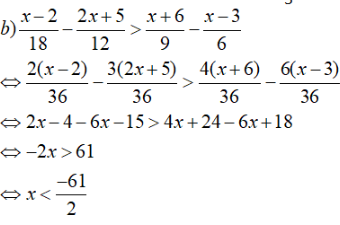
Vậy tập nghiệm của bất phương trình là