1 Chứng minh: BFCP là hình bình hình.
2) Tia DM cắt tia BP tại Q. Chứng minh: DPQF là hình chữ nhật.
3) Chứng minh: Tam giác EBP cân
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Hướng dẫn giải
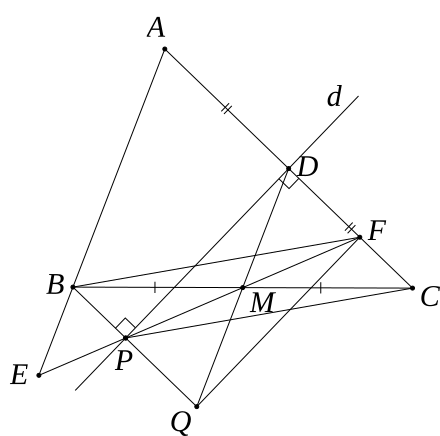
1) Ta có:
BP ⊥ d (gt)
CF ⊥ d (do d là đường trung trực AC)
⇒ BP // CF
Xét ΔBMP và ΔCMF có:
\(\widehat {BMP} = \widehat {FMC}\) (đối đỉnh)
BM = MC (gt)
\(\widehat {PBM} = \widehat {MCF}\) (so le trong)
⇒ ΔBMP = ΔCMF (g.c.g)
⇒ PM = MF
Xét tứ giác BPCF có:
PM = MF (cmt)
BM = MC (do M là trung điểm BC)
⇒ Tứ giác BPCF là hình bình hành (2 đường chéo cắt nhau tại trung điểm của mỗi đường)
2) Xét ΔPMQ và ΔFMD có:
\(\widehat {PMQ} = \widehat {FMD}\)(cmt)
PM = MF (cmt)
\(\widehat {MPQ} = \widehat {MFD}\) (do BP // CF, so le trong)
⇒ ΔPMQ = ΔFMD (g.c.g)
⇒ QM = MD
⇒ M là trung điểm QD
Xét tứ giác DPQF có
M là trung điểm của QD (cmt)
M là trung điểm của PF (cmt)
⇒Tứ giác DPQF là hình bình hành
Lại có: PD ⊥ DF (do d là đường trung trực của AC mà PD thuộc d và DF thuộc AC)
Hình bình hành DPQF có một góc vuông
⇒ DPQF là hình chữ nhật
3) Ta có: DPQF là hình chữ nhật
⇒ PF = QD (2 đường chéo của hình chữ nhật) và PM = QM (=1/2 PF = 1/2 QD)
Xét ΔPMQ có PM = QM ⇒ ΔPMQ cân tại M
\( \Rightarrow \widehat {MPQ} = \widehat {MQP}\) (1)
Tứ giác BPCF là hình bình hành ⇒ BP = CF
Tứ giác DPQF là hình chữ nhật ⇒ PQ = DF
Suy ra BP + PQ = CF + DF ⇒ BQ = DC
Mà DC = AD (vì D là trung điểm của AC)
Xét tứ giác ADQB có AD = BQ và AD//BQ
⇒ ADQB là hình bình hành
⇒ AB // QD
\( \Rightarrow \widehat {EBP} = \widehat {MQP}\) (so le trong (2)
Ta có : \(\widehat {BPE} = \widehat {MPQ}\) (đối đỉnh) (3)
Từ (1), (2), (3) \( \Rightarrow \widehat {BPE} = \widehat {EBP}\)
Xét ΔEBP có: \(\widehat {BPE} = \widehat {EBP}\) (cmt)
⇒ ΔEBP cân tại E
A = x3+ y3+ 2xy.
1) A = x2– 5x + 4;
2) B = 9x2+ 4y2– 12xy – 4;