Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B và có AB = BC = a, AD = 2a có SA vuông góc với đáy và SA = a. Gọi M, N lần lượt là trung điểm của SB và CD. Tính cosin của góc giữa MN và (SAC)
A. .
B. .
C. .
D. .
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Chọn hệ trục tọa độ như hình vẽ.
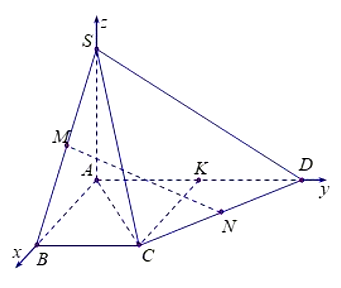
Khi đó
Do M, N lần lượt là trung điểm của SB, CD nên M, N có tọa độ lần lượt là:
là vectơ chỉ phương của đường thẳng MN.
Gọi K là trung điểm của là hình bình hành.
Suy ra: Tam giác ACD vuông tại C.
Ta có
Mà: là vectơ pháp tuyến của .
Gọi là góc giữa MN và .
Ta có:
Chọn A.
Cho hình lăng trụ ABC.A'B'C' có mặt đáy ABC là tam giác đều cạnh AB = 2a. Hình chiếu vuông góc của A' lên mặt phẳng (ABC) trùng với trung điểm H của AB. Biết góc giữa cạnh bên và mặt đáy bằng 600. Tính theo a khoảng cách H từ điểm B đến mặt phẳng (ACC'A').
Có bao nhiêu giá trị nguyên của tham số sao cho hàm số nghịch biến trên khoảng ?
Cho hàm số f(x) liên tục trên và có đồ thị như hình vẽ bên dưới.
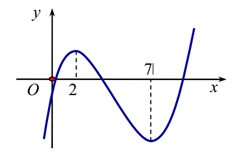
Khẳng định nào sau đây là đúng?
Cho cấp số cộng có số hạng tổng quát là Tìm công sai d của cấp số cộng.
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng và đường thẳng Viết phương trình đường thẳng đi qua A(1;-1;2) đồng thời vuông góc với cả hai đường thẳng d1 và d2.
Thể tích của khối nón có chiều cao bằng 4 và đường sinh bằng 5 bằng