Cho tam giác ABC vuông tại A, AB = 3 cm, BC = 5 cm. Trên cạnh BC lấy điểm D sao cho BD = 3 cm. Đường thẳng vuông góc với BC tại D cắt cạnh AC tại M, cắt tia BA tại N.
a) Tính AC và so sánh các góc của tam giác ABC.
b) Chứng minh MA = MD và tam giác MNC cân.
c) Gọi I là trung điểm của CN. Chứng minh ba điểm B, M, I thẳng hàng.
Giải bởi qa.haylamdo.com
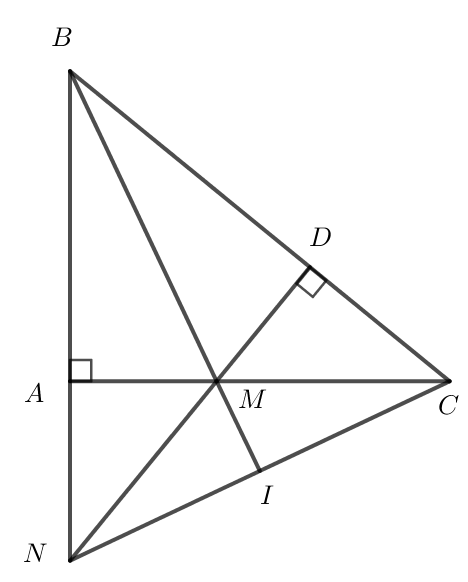
a) Áp dụng định lý Pytago vào tam giác ABC vuông tại A:
AB2 + AC2 = BC2
32 + AC2 = 52
AC2 = 25 - 9
AC2 = 16
AC = 4 cm.
vuông tại A nên là góc lớn nhất trong
AB < AC nên .
Vậy
b) Xét vuông tại A và vuông tại D có:
AB = BD (theo giả thiết)
BM chung.
(cạnh huyền - cạnh góc vuông).
MA = MD (2 cạnh tương ứng).
Xét vuông tại A và cân tại D có:
AM = DM (chứng minh trên).
(2 góc đối đỉnh).
(góc nhọn - cạnh góc vuông).
MN = MC (2 cạnh tương ứng).
có MN = MC nên cân tại M.
c) Xét có .
Mà CA cắt ND tại M nên M là trực tâm của .
Do đó (1).
cân tại M, lại có I là trung điểm của NC nên (2).
Từ (1) và (2) suy ra B, M, I thẳng hàng.
Cho tam giác ABC cân tại A có AB = 5 cm, BC = 6 cm và AM là đường trung tuyến. Độ dài đoạn AM là:
a) Tính giá trị biểu thức: 4x3 - 3xy tại x = ; y = 6.
b) Cho đơn thức A = (-3xy) . . Hãy thu gọn đơn thức và chỉ ra hệ số, phần biếnTìm tất cả nghiệm của mỗi đa thức sau:
a) A = 2(-x + 5) - 
(x - 4).
b) B = -4x2 + 9.
c) C = x3 + 4x.
