Cho tam giác ABC vuông tại A. Vẽ đường thẳng d đi qua A và song song với đường thẳng BC, BH vuông góc với d tại H.

a) Chứng minh ∆ABC∆HAB.

b) Gọi K là hình chiếu của C trên d. Chứng minh AH.AK = BH.CK.

c) Gọi M là giao điểm của hai đoạn thẳng AB và HC. Tính độ dài đoạn thẳng HA và diện tích ∆MBC, khi AB = 3cm, AC = 4cm, BC = 5cm.

GT	∆ABC vuông tại A; Đường thẳng d đi qua A, d // BC; $BH\perp d(H\in d)$; K là hình chiếu của C trên d; $AB\cap HC=M$; AB = 3cm, AC = 4cm, BC = 5cm.
KL	a) ∆ABC  ∆HAB. b) AH.AK = BH.CK. c) Tính độ dài HA và diện tích ∆MBC.

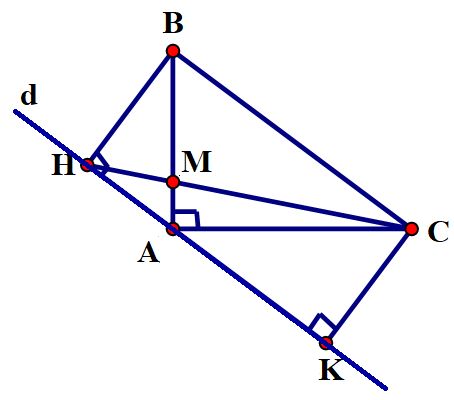
a) Ta có $\widehat{BAC}={90}^o$ (vì ∆ABC vuông tại A) và $\widehat{AHB}={90}^o$ (AH ^ BH)

Nên $\widehat{BAC}=\widehat{AHB}={90}^o$.

Xét ∆ABC và ∆HAB có:

$\widehat{BAC}=\widehat{AHB}={90}^o$ (cmt)

$\widehat{ABC}=\widehat{BAH}$ (d // BC, hai góc so le trong)

Do đó ∆ABC∆HAB (g.g).

b) Ta có $\widehat{AKC}={90}^o$ (vì K là hình chiếu của C trên d) nên $\widehat{AHB}=\widehat{AKC}={90}^o$.

Lại có $\widehat{CAK}+\widehat{BAH}=\widehat{BAC}={90}^o$;

$\widehat{BAH}+\widehat{ABH}={90}^o$(∆HAB vuông ở H)

Do đó $\widehat{CAK}=\widehat{ABH}$.

Xét ∆HAB và ∆KCA có:

$\widehat{AHB}=\widehat{AKC}={90}^o$ (cmt)

$\widehat{CAK}=\widehat{ABH}$ (cmt)

Do đó ∆HAB ∆KCA (g.g)

Suy ra $\frac{HA}{KC}=\frac{HB}{KA}$ Û AH.AK = BH.CK (đpcm).

c) Từ câu a: ∆ABC  ∆HAB $\Rightarrow \frac{BC}{AB}=\frac{AB}{HA}$$\iff \frac{5}{3}=\frac{3}{HA}$ 

$\Rightarrow HA=\frac{3.3}{5}=\frac{9}{5}\left(cm\right)$.

Ta có AH // BC, áp dụng định lý Ta-let: $\frac{BC}{AH}=\frac{BM}{MA}$ 

$\Rightarrow AM=\frac{AH.BM}{BC}=\frac{\frac{9}{5}.BM}{5}=\frac{9}{25}BM$.

Lại có AM + BM = AB = 3 (cm).

$\Rightarrow AB=\frac{9}{25}BM+BM=\frac{34}{25}BM=3$

$\Rightarrow BM=\frac{75}{34}\left(cm\right)$

Diện tích tam giác MBC là:

$S_{MBC}=\frac{1}{2}.AC.MB=\frac{1}{2}.4.\frac{75}{34}=\frac{75}{17}$ (cm²).