A. f(x) liên tục tại x0=0.
B. limx→0+f(x)=1
C. f(0) = 0
D. limx→0−f(x)=0
Giải bởi qa.haylamdo.com
Phương pháp:
- Tính các giới hạn limx→0+f(x),limx→0−f(x).
- Hàm số y = f(x) liên tục tại x=x0 khi và chỉ khi limx→x+0f(x)=limx→x−0f(x)=f(x0)
Cách giải:
Ta có:
limx→0+f(x)=limx→0(x2+1)=1
limx→0−f(x)=limx→0−(x)=0
⇒ Đáp án B, D đúng.
Vì limx→0+f(x)≠limx→0−f(x)⇒ Hàm số gián đoạn tại x0=0 nên đáp án A sai.
Chọn A.
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình (S):x2+y2+z2−2x−4y−6z+5=0. Tính diện tích mặt cầu (S)
Đường tiệm cận đứng của đồ thị hàm số y=−3x+1x−1 có phương trình là:
Cho hàm số y = f(x) xác định và có đạo hàm cấp một và cấp hai trên khoảng (a; b) và x0∈(a;b). Khẳng định nào sau đây sai?
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa hai mặt phẳng (SCD) và (ABCD) bằng φ và sinφ=√55. Khoảng cách từ điểm A đến mặt phẳng (SCD) bằng:
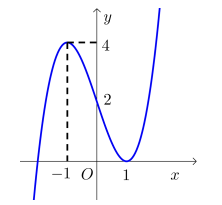
Cho hàm số f(x) có đạo hàm liên tục trên ℝ và có đồ thị như hình vẽ bên. Số đường tiệm cận đứng của đồ thị hàm số y=x2−1f2(x)−5f(x)
Một khối trụ có diện tích xung quanh bằng 80π. Tính thể tích của khối trụ biết khoảng cách giữa hai đáy bằng 10.
Biết hàm số f(x) - f(2x) có đạo hàm bằng 20 tại x = 1 và đạo hàm bằng 1001 tại x = 2. Tính đạo hàm của hàm số
f(x) - f(4x) tại x = 1.
