Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa hai mặt phẳng (SCD) và (ABCD) bằng và . Khoảng cách từ điểm A đến mặt phẳng (SCD) bằng:
A.
B.
C.
D.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Phương pháp:
- Gọi H là trung điểm của AB. Chứng minh .
- Xác định góc giữa (SCD) và (ABCD) bằng góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.
- Chứng minh , dựng .
- Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông tính .
Cách giải:
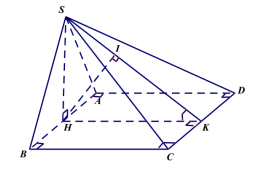
Gọi H là trung điểm của AB. Vì tam giác SAB cân tại S nên .
Ta có:
Gọi K là trung điểm của CD ta có
Vì .
Trong (SHK) kẻ ta có:
Xét tam giác vuông HIK ta có
Vậy
Chọn C.
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình Tính diện tích mặt cầu (S)
Cho hàm số y = f(x) xác định và có đạo hàm cấp một và cấp hai trên khoảng (a; b) và Khẳng định nào sau đây sai?
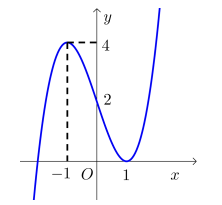
Cho hàm số f(x) có đạo hàm liên tục trên và có đồ thị như hình vẽ bên. Số đường tiệm cận đứng của đồ thị hàm số
Một khối trụ có diện tích xung quanh bằng Tính thể tích của khối trụ biết khoảng cách giữa hai đáy bằng 10.
Biết hàm số f(x) - f(2x) có đạo hàm bằng 20 tại x = 1 và đạo hàm bằng 1001 tại x = 2. Tính đạo hàm của hàm số
f(x) - f(4x) tại x = 1.