Đọc đoạn trích sau đây và trả lời các câu hỏi:
Rời khỏi kinh thành, sông Hương chếch về hướng chính bắc, ôm lấy đảo Cồn Hến quanh năm mơ màng trong sương khói, đang xa dần thành phố để lưu luyến ra đi giữa màu xanh của tre trúc và của những vườn cau vùng ngoại ô Vĩ Dạ. Và rồi, như sực nhớ lại một điều gì chưa kịp nói, nó đột ngột đổi dòng, rẽ ngoặt sang hướng đông tây để gặp lại thành phố lần cuối ở góc thị trấn Bao Vinh xưa cổ. Đối với Huế, nơi đây chính là chỗ chia tay dõi xa ngoài mười dặm trường đình.
(Trích Ai đã đặt tên cho dòng sông – Hoàng Phủ Ngọc Tường, Ngữ văn 12, Tập một, NXB Giáo dục)
Vẻ đẹp của con sông Hương được tác giả miêu tả dưới góc nhìn nào?D. Góc nhìn cổ tích
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Đáp án A
Phương pháp giải:
Căn cứ vào nội dung của tác phẩm
Giải chi tiết:
Vẻ đẹp con sông Hương trong đoạn trích trên được cảm nhận dưới góc nhìn địa ý.
Tiến hành thí nghiệm theo các bước sau:
Bước 1: Cho vào hai bình cầu mỗi bình khoảng 6 ml metyl axetat.
Bước 2: Thêm khoảng 6 - 8 ml dung dịch H2SO4 loãng 25% vào bình thứ nhất, khoảng 12 ml dung dịch NaOH 35% vào bình thứ hai.
Bước 3: Lắc đều cả hai bình, lắp ống sinh hàn rồi đun sôi nhẹ trong khoảng thời gian 5 - 8 phút, sau đó để nguội.
Phát biểu nào sau đây đúng?
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {\left( {x - 1} \right)^3}\left[ {{x^2} + \left( {4m - 5} \right)x + {m^2} - 7m + 6} \right],{\mkern 1mu} {\mkern 1mu} \forall x \in \mathbb{R}\). Có bao nhiêu số nguyên m để hàm số \(g\left( x \right) = f\left( {\left| x \right|} \right)\) có đúng 5 điểm cực trị?
Tiếp tuyến của đồ thị hàm số \(y = \frac{{x + 1}}{{2x - 3}}\) tại điểm có hoành độ \({x_0} = - 1\) có hệ số góc bằng bao nhiêu?
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( P \right):{\mkern 1mu} {\mkern 1mu} 3x - y + z - 7 = 0\). Phương trình đường thẳng \(\Delta \) đi qua điểm \(A\left( {2; - 3;1} \right)\) và vuông góc với mặt phẳng \(\left( P \right)\) là:
Nung 0,935 gam quặng cromit với chất oxi hóa để oxi hóa toàn bộ crom thành CrO42-. Hòa tan sản phẩm vào nước, phân hủy hết chất oxi hóa, axit hóa dung dịch bằng H2SO4 rồi thêm 50,0 ml dung dịch FeSO4 0,08M vào. Để chuẩn độ FeSO4 dư cần 14,85 ml dung dịch KMnO4 0,004M. Hàm lượng crom có trong quặng là
Cho hàm số \(y = f\left( x \right)\) liên tục trên tập số thực thỏa mãn \(f\left( x \right) + \left( {5x - 2} \right)f\left( {5{x^2} - 4x} \right)\) \( = 50{x^3} - 60{x^2} + 23x - 1\) \(\forall x \in \mathbb{R}\). Giá trị của biểu thức \(\int\limits_0^1 {f\left( x \right)dx} \) bằng:
Pha chế 35,8 gam dung dịch CuSO4 bão hòa ở 100oC. Đun nóng dung dịch này cho đến khi có 17,86 gam nước bay hơi, sau đó để nguội đến 20oC. Tính số gam tinh thể CuSO4.5H2O kết tinh. Biết rằng độ tan của CuSO4 trong nước ở 20oC và 100oC lần lượt là 20,26 gam và 75,4 gam.
Tìm nghiệm của phương trình \({\log _2}\left( {x - 5} \right) = 4\).
Este X hai chức, mạch hở, tạo bởi một ancol no với hai axit cacboxylic no, đơn chức. Este Y ba chức, mạch hở tạo bởi glixerol với một axit cacboxylic không no, đơn chức (phân tử có hai liên kết π). Đốt cháy hoàn toàn m gam hỗn hợp E gồm X và Y cần vừa đủ 0,5 mol O2 thu được 0,45 mol CO2. Mặt khác, thủy phân hoàn toàn 0,16 mol E cần vừa đủ 210 ml dung dịch NaOH 2M thu được hai ancol (có cùng số nguyên tử cacbon trong phân tử) và hỗn hợp ba muối, trong đó tổng khối lượng hai muối của hai axit no là a gam. Giá trị của a là
Cho tứ diện \[ABCD\] có \(AB,{\mkern 1mu} {\mkern 1mu} AC,{\mkern 1mu} {\mkern 1mu} AD\) đôi một vuông góc với \(AB = 6a\), \(AC = 9a\), \(AD = 3a\). Gọi \(M,{\mkern 1mu} {\mkern 1mu} N,{\mkern 1mu} {\mkern 1mu} P\) lần lượt là trọng tâm các tam giác \(ABC,{\mkern 1mu} {\mkern 1mu} ACD,{\mkern 1mu} {\mkern 1mu} ADB\). Thể tích của khối tứ diện \(AMNP\) bằng:
Tiến hành thí nghiệm như hình vẽ:
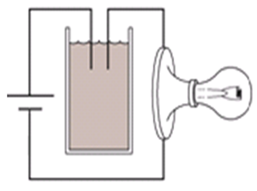
Ban đầu trong cốc chứa nước vôi trong. Sục rất từ từ CO2 vào cốc cho tới dư. Hỏi độ sáng của bóng đèn thay đổi như thế nào?