Top 5 đề thi Đánh giá năng lực trường ĐHQG Hà Nội có đáp án (Đề 4)
-
3921 lượt thi
-
150 câu hỏi
-
195 phút
Danh sách câu hỏi
Câu 1:
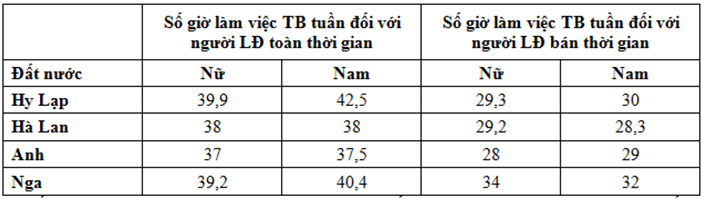
Ở quốc gia nào, số giờ làm việc trung bình của người lao động nữ cao hơn những quốc gia còn lại?
Đáp án D
Phương pháp giải:
Tính số giờ làm việc trung bình của nữ (lao động toàn thời gian và bán thời gian) ở mỗi quốc gia, sau đó kết luận.
Giải chi tiết:
Số giờ làm việc trung bình của nữ (lao động toàn thời gian và bán thời gian) ở:
Hy Lạp: \(\frac{{39,9 + 29,3}}{2} = 34,6\) (giờ)
Hà Lan: \(\frac{{38 + 29,2}}{2} = 33,6\) (giờ)
Anh: \(\frac{{37 + 28}}{2} = 32,5\) (giờ)
Nga: \(\frac{{39,2 + 34}}{2} = 36,6\) (giờ)
Vậy số giờ làm việc trung bình của nữ (lao động toàn thời gian và bán thời gian) ở Nga cao hơn những quốc gia còn lại.
Câu 2:
Cho chuyển động xác định bởi phương trình \(S\left( t \right) = \frac{{ - 1}}{4}{t^4} + 3{t^2} - 2t - 4\), trong đó t tính bằng giây (s) và S tính bằng mét (m). Tại thời điểm nào, giá tốc của chuyển động đạt giá trị lớn nhất?
Đáp án D
Phương pháp giải:
- Tính gia tốc \(a\left( t \right) = S''\left( t \right)\).
- Hàm số \(y = a{x^2} + bx + c{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {a < 0} \right)\) đạt giá trị lớn nhất tại \(x = - \frac{b}{{2a}}\).
Giải chi tiết:
Ta có: \(S'\left( t \right) = - {t^3} + 6t - 2\)
\(S''\left( t \right) = - 3{t^2} + 6\)
\( \Rightarrow a\left( t \right) = S''\left( t \right) = - 3{t^2} + 6\)
Do đồ thị hàm số \(y = - 3{t^2} + 6\) có dạng parabol có bề lõm hướng xuống nên đạt GTLN tại \(x = - \frac{b}{{2a}} = 0\).
Khi đó \(a{\left( t \right)_{\max }} = 6 \Leftrightarrow t = 0\).
Câu 3:
Tìm nghiệm của phương trình \({\log _2}\left( {x - 5} \right) = 4\).
Đáp án C
Phương pháp giải:
Giải phương trình lôgarit: \({\log _a}f\left( x \right) = n \Leftrightarrow f\left( x \right) = {a^n}\)
Giải chi tiết:
Ta có: \({\log _2}\left( {x - 5} \right) = 4 \Leftrightarrow x - 5 = {2^4} = 16 \Leftrightarrow x = 21\).
Câu 4:
Nghiệm của hệ phương trình \(\left\{ \begin{array}{l}\sqrt {\frac{{1 - x}}{{2y + 1}}} + \sqrt {\frac{{2y + 1}}{{1 - x}}} = 2\\x - y = 1\end{array} \right.\) là
Đáp án D
Phương pháp giải: :
+) Tìm điều kiện của x và y để biểu thức trong căn có nghĩa.
+) Biểu diễn x theo y và thay vào phương trình còn lại ta được một phương trình chứa căn thức với ẩn là y. Tiếp theo, ta đặt ẩn phụ để giải, thay ngược lại để tìm được giá trị của x và y.
+) Khi tìm được nghiệm x và y ta đối chiếu với điều kiện xác định và kết luận nghiệm của hệ phương trình.
Giải chi tiết:
Đk: \(\left\{ {\begin{array}{*{20}{l}}{\frac{{1 - x}}{{2y + 1}} \ge 0}\\{\frac{{2y + 1}}{{1 - x}} \ge 0}\\{y \ne \frac{{ - 1}}{2}}\\{x \ne 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\frac{{1 - x}}{{2y + 1}} > 0}\\{\frac{{2y + 1}}{{1 - x}} > 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{l}}{1 - x > 0}\\{2y + 1 > 0}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{l}}{1 - x < 0}\\{2y + 1 < 0}\end{array}} \right.}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{l}}{x < 1}\\{y > \frac{{ - 1}}{2}}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{l}}{x > 1}\\{y < \frac{{ - 1}}{2}}\end{array}} \right.}\end{array}} \right..\)
\(\left\{ {\begin{array}{*{20}{l}}{\sqrt {\frac{{1 - x}}{{2y + 1}}} + \sqrt {\frac{{2y + 1}}{{1 - x}}} = 2{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 1 \right)}\\{x - y = 1{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 2 \right)}\end{array}} \right.\)
Từ (2) suy ra: \(x = 1 + y\) thay vào (1) ta có:
PT \( \Leftrightarrow \sqrt {\frac{{1 - 1 - y}}{{2y + 1}}} + \sqrt {\frac{{2y + 1}}{{1 - 1 - y}}} = 2 \Leftrightarrow \sqrt {\frac{{ - y}}{{2y + 1}}} + \sqrt {\frac{{2y + 1}}{{ - y}}} = 2{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 3 \right)\)
Đặt \(\frac{{ - y}}{{2y + 1}} = t\left( {t \ge 0} \right) \Rightarrow \frac{{2y + 1}}{{ - y}} = \frac{1}{t}\) khi đó (3) có dạng:
\(\frac{{ - y}}{{2y + 1}} = 1 \Leftrightarrow 2y + 1 = - y \Leftrightarrow 3y = 1 \Leftrightarrow y = \frac{1}{3} \Rightarrow x = 1 + \frac{1}{3} = \frac{4}{3}\)
\(\sqrt t + \sqrt {\frac{1}{t}} = 2 \Leftrightarrow t + 2 + \frac{1}{t} = 4 \Leftrightarrow {t^2} - 2t + 1 = 0 \Leftrightarrow {\left( {t - 1} \right)^2} = 0 \Leftrightarrow t = 1\left( {tm} \right)\)
Suy ra: \(\frac{{ - y}}{{2y + 1}} = 1 \Leftrightarrow 2y + 1 = - y \Leftrightarrow y = \frac{1}{3}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {tm} \right) \Rightarrow x = \frac{1}{3} + 1 = \frac{4}{3}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {ktm} \right)\).
Vậy hệ phương trình vô nghiệm.
Câu 5:
Trong mặt phẳng tọa độ \(Oxy\), cho điểm \(M,N,P\) lần lượt là điểm biểu diễn của các số phức \(2 + 3i,1 - 2i, - 3 + i\). Tọa độ điểm \(Q\) sao cho tứ giác \(MNPQ\) là hình bình hành là
Đáp án C
Phương pháp giải:
- Điểm \(M\left( {a;b} \right)\) biểu diễn số phức \(z = a + bi\).
- Tứ giác \(ABCD\) là hình bình hành \( \Leftrightarrow \overrightarrow {AB} = \overrightarrow {DC} \).
Giải chi tiết:
Ta có: các điểm \(M\left( {2;3} \right),N\left( {1; - 2} \right),P\left( { - 3;1} \right)\) lần lượt biểu diễn các số phức \(2 + 3i,{\mkern 1mu} {\mkern 1mu} 1 - 2i,{\mkern 1mu} {\mkern 1mu} - 3 + i\).
Gọi điểm \(Q\left( {x;y} \right)\) thì tứ giác \(MNPQ\) là hình bình hành
\( \Leftrightarrow \overrightarrow {MN} = \overrightarrow {QP} \)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{1 - 2 = - 3 - x}\\{ - 2 - 3 = 1 - y}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = - 2}\\{y = 6}\end{array}} \right. \Rightarrow Q\left( { - 2;6} \right)\).
Câu 6:
Trong không gian \(Oxyz\) cho \(A\left( {1;1; - 2} \right),B\left( {2;0;3} \right),C\left( { - 2;4;1} \right)\). Mặt phẳng đi qua A và vuông góc với đường thẳng BC có phương trình là:
Đáp án B
Phương pháp giải:
- Mặt phẳn đi qua A và vuông góc với đường thẳng BC nhận \(\overrightarrow {BC} \) là 1 VTPT.
- Phương trình mặt phẳng đi qua \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) và có 1 VTPT \(\vec n\left( {a;b;c} \right) \ne \vec 0\) là:
\(a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) + c\left( {z - {z_0}} \right) = 0\).
Ta có: \(\overrightarrow {BC} = \left( { - 4;4; - 2} \right)\) là 1 VTPT của mặt phẳng qua A và vuông góc với đường thẳng BC.
Mặt phẳng đi qua A và vuông góc với đường thẳng BC nhận \(\overrightarrow {BC} = \left( { - 4;4; - 2} \right)\) là VTPT, có phương trình là: \( - 4\left( {x - 1} \right) + 4\left( {y - 1} \right) - 2\left( {z + 2} \right) = 0\)
\( \Leftrightarrow - 4x + 4y - 2z - 4 = 0\)
\( \Leftrightarrow 2x - 2y + z + 2 = 0\).
Câu 7:
Đáp án B
Phương pháp giải:
Hình chiếu vuông góc của điểm \(M\left( {{x_0};{\mkern 1mu} {\mkern 1mu} {y_0};{\mkern 1mu} {\mkern 1mu} {z_0}} \right)\) trên mặt phẳng \(\left( {Oyz} \right)\) là \(M'\left( {0;{\mkern 1mu} {\mkern 1mu} {y_0};{\mkern 1mu} {\mkern 1mu} {z_0}} \right)\).
Giải chi tiết:
Hình chiếu vuông góc của điểm \(M\left( {1; - 2;{\mkern 1mu} {\mkern 1mu} 3} \right)\) trên mặt phẳng \(\left( {Oyz} \right)\) là \(A\left( {0;{\mkern 1mu} - 2;{\mkern 1mu} {\mkern 1mu} 3} \right).\)
Câu 8:
Bất phương trình \(2x + \frac{3}{{2x - 4}} < 3 + \frac{3}{{2x - 4}}\) tương đương với
Đáp án D
Phương pháp giải:
Sử dụng định nghĩa: Hai bất phương trình được gọi là tương đương nếu chúng có cùng tập nghiệm.
Giải chi tiết:
ĐKXĐ: \(2x - 4 \ne 0 \Leftrightarrow x \ne 2\)
\(2x + \frac{3}{{2x - 4}} < 3 + \frac{3}{{2x - 4}}\)
\( \Leftrightarrow 2x < 3\)
\( \Leftrightarrow x < \frac{3}{2}\)
Kết hợp với điều kiện \(x \ne 2\), bất phương trình \( \Leftrightarrow x < \frac{3}{2}\).
Câu 9:
Phương trình \({\sin ^2}x + \sqrt 3 \sin x\cos x = 1\) có bao nhiêu nghiệm thuộc \(\left[ {0;3\pi } \right]\).
Đáp án B
Phương pháp giải:
Xét hai trường hợp:
TH1: \(\cos x = 0\)
TH2: \(\cos x \ne 0\). Chia cả 2 vế của phương trình cho \({\cos ^2}x\).
Giải chi tiết:
TH1: \(\cos x = 0 \Leftrightarrow x = \frac{\pi }{2} + k\pi {\mkern 1mu} {\mkern 1mu} \left( {k \in Z} \right) \Rightarrow {\sin ^2}x = 1\), khi đó phương trình trở thành \(1 = 1\) (luôn đúng).
\( \Rightarrow x = \frac{\pi }{2} + k\pi {\mkern 1mu} {\mkern 1mu} \left( {k \in Z} \right)\) là nghiệm của phương trình.
\(x \in \left[ {0;3\pi } \right] \Rightarrow 0 \le \frac{\pi }{2} + k\pi \le 3\pi \Leftrightarrow - \frac{1}{2} \le k \le \frac{5}{2}{\mkern 1mu} \left( {k \in Z} \right) \Leftrightarrow k \in \left\{ {0;1;2} \right\}\).
TH2: \(\cos x \ne 0 \Leftrightarrow x \ne \frac{\pi }{2} + k\pi {\mkern 1mu} {\mkern 1mu} \left( {k \in Z} \right)\). Chia cả 2 vế của phương trình cho \({\cos ^2}x\) ta được:
\(\frac{{{{\sin }^2}x}}{{{{\cos }^2}x}} + \sqrt 3 \frac{{\sin x}}{{\cos x}} = \frac{1}{{{{\cos }^2}x}} \Leftrightarrow {\tan ^2}x + \sqrt 3 \tan x = 1 + {\tan ^2}x \Leftrightarrow \tan x = \frac{1}{{\sqrt 3 }} \Leftrightarrow x = \frac{\pi }{6} + k\pi {\mkern 1mu} {\mkern 1mu} \left( {k \in Z} \right)\)
\(x \in \left[ {0;3\pi } \right] \Rightarrow 0 \le \frac{\pi }{6} + k\pi \le 3\pi \Leftrightarrow - \frac{1}{6} \le k \le \frac{{17}}{6}{\mkern 1mu} \left( {k \in Z} \right) \Leftrightarrow k \in \left\{ {0;1;2} \right\}\)
Vậy phương trình đã cho có 6 nghiệm thỏa mãn yêu cầu bài toán.
Câu 10:
Trên một cái bảng đã ghi sẵn các số tự nhiên từ 1 đến 2020. Ta thực hiện công việc như sau: xóa hai số bất kì trên bảng rồi ghi lại một số tự nhiên bằng tổng của hai số vừa xóa, cứ thực hiện công việc như vậy cho đến khi trên bảng chỉ còn một số. Số cuối cùng còn lại trên bảng là:
Đáp án B
Phương pháp giải:
Sử dụng công thức tính tổng \(1 + 2 + ... + n = \frac{{n\left( {n + 1} \right)}}{2}\).
Giải chi tiết:
Thực hiện liên tiếp việc xóa hai số bất kì trên bảng rồi ghi lại một số tự nhiên bằng tổng của hai số vừa xóa, cứ thực hiện công việc như vậy cho đến khi trên bảng chỉ còn một số. Số cuối cùng còn lại trên bảng sẽ là tổng của các số tự nhiên từ 1 đến 2020.
Vậy số còn lại trên bảng là \(1 + 2 + ... + 2020 = \frac{{2020.2021}}{2} = 2041210\).
Câu 11:
Họ nguyên hàm \(\int {\frac{{{x^2} + 2x + 3}}{{x + 1}}dx} \) bằng:
Đáp án C
Phương pháp giải:
Sử dụng phương pháp tính nguyên hàm của hàm số hữu tỷ có bậc tử cao hơn bậc mẫu, ta chia tử cho mẫu sau đó sử dụng các công thức nguyên hàm của hàm số cơ bản để tìm nguyên hàm của hàm số.
Giải chi tiết:
\(\int {\frac{{{x^2} + 2x + 3}}{{x + 1}}dx} = \int {\frac{{{x^2} + 2x + 1 + 2}}{{x + 1}}dx} \)
\( = \int {\frac{{{{\left( {x + 1} \right)}^2} + 2}}{{x + 1}}dx} = \int {\left( {x + 1} \right)dx} + \int {\frac{2}{{x + 1}}dx} \)
\( = \frac{{{x^2}}}{2} + x + 2\ln \left| {x + 1} \right| + C\).
Câu 12:
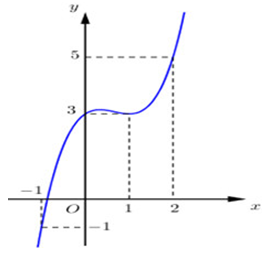
Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của m để phương trình \(f\left( {2 - \sqrt {2x - {x^2}} } \right) = m\) có nghiệm?
Đáp án C
Phương pháp giải:
+) Đặt \(t\left( x \right) = 2 - \sqrt {2x - {x^2}} ,{\mkern 1mu} {\mkern 1mu} x \in \left[ {0;2} \right]\), tìm khoảng giá trị của \(t\).
+) Dựa vào đồ thị hàm số, tìm điều kiện của \(m\) để phương trình \(f\left( t \right) = m\) có nghiệm thỏa mãn ĐK tìm được ở bước trên.
Giải chi tiết:
Xét hàm số \(t\left( x \right) = 2 - \sqrt {2x - {x^2}} ,{\mkern 1mu} {\mkern 1mu} x \in \left[ {0;2} \right]\), có:
\(t'\left( x \right) = \frac{{x - 1}}{{\sqrt {2x - {x^2}} }};{\mkern 1mu} {\mkern 1mu} t'\left( x \right) = 0 \Leftrightarrow x = 1\)
Hàm số \(t\left( x \right)\) liên tục trên \(\left[ {0;2} \right]\) có:
\(t\left( 0 \right) = t\left( 2 \right) = 2,{\mkern 1mu} {\mkern 1mu} t\left( 1 \right) = 1 \Rightarrow \mathop {\min }\limits_{\left[ {0;2} \right]} t\left( x \right) = 1,{\mkern 1mu} {\mkern 1mu} \mathop {\max }\limits_{\left[ {0;2} \right]} t\left( x \right) = 2\)
\(x \in \left[ {0;2} \right] \Rightarrow t \in \left[ {1;2} \right]\). Khi đó bài toán trở thành có bao nhiêu giá trị nguyên của m để phương trình \(f\left( t \right) = m\) có nghiệm \(t \in \left[ {1;2} \right]\).
Quan sát đồ thị hàm số \(y = f\left( t \right)\) trên đoạn \(\left[ {1;2} \right]\) ta thấy, phương trình \(f\left( t \right) = m\) có nghiệm \( \Leftrightarrow 3 \le m \le 5\).
Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ {3;4;5} \right\}\) có 3 giá trị của m thỏa mãn.
Câu 13:
Một ô tô đang chạy với vận tốc \(15\left( {m/s} \right)\) thì tăng tốc chuyển động nhanh dần với gia tốc \(a = 3t - 8{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {m/{s^2}} \right)\), trong đó t là khoảng thời gian tính bằng giây kể từ lúc tăng tốc. Hỏi sau 10 giây tăng vận tốc ô tô đi được bao nhiêu mét?
Đáp án D
Phương pháp giải:
- Tìm hàm số vận tốc: \(v\left( t \right) = \int {a\left( t \right)dt} \), sử dụng dữ kiện \(v\left( 0 \right) = 15\) để tìm C.
- Quãng đường đi được sau 10 giây là: \(S = \int\limits_0^{10} {v\left( t \right)dt} \).
Giải chi tiết:
Ta có \(v = \int {a\left( t \right)dt = \int {\left( {3t - 8} \right)dt} } = \frac{{3{t^2}}}{2} - 8t + C\).
Vì ô tô đang chạy với vận tốc 15m/s nên ta có: \(v\left( 0 \right) = 15 \Rightarrow C = 15.\)
\( \Rightarrow v = \frac{{3{t^2}}}{2} - 8t + 15.\)
Vậy quãng đường ô tô đi được sau 10 giây là: \(S = \int\limits_0^{10} {\left( {\frac{{3{t^2}}}{2} - 8t + 15} \right)dt = 250} \).
Câu 14:
Một người gửi 300 triệu đồng vào ngân hàng theo thể thức lãi kép kì hạn 1 quý và lãi suất 1,75% một quý. Hỏi sau ít nhất bao nhiêu tháng người gửi có ít nhất 500 triệu đồng (bao gồm cả vốn lẫn lãi) từ số vốn ban đầu? (Giả sử lãi suất không thay đổi).
Đáp án D
Phương pháp giải:
Sử dụng công thức lãi kép \(T = A{\left( {1 + r} \right)^N}\).
Số tiền người đó nhận được sau \(N\) quý là: \(T = 300{\left( {1 + 1,75\% } \right)^N}\)
Ta có: \(T \ge 500 \Leftrightarrow 300{\left( {1 + 1,75\% } \right)^N} \ge 500\)
\( \Leftrightarrow 1,{0175^N} \ge \frac{5}{3} \Leftrightarrow N \ge {\log _{1,0175}}\frac{5}{3} \approx 29,445\).
Do \(N\) là nhỏ nhất nên \(N = 30\) quý.
Do đó sau \(30.3 = 90\) tháng thì người đó có ít nhất 500 triệu.
Câu 15:
Tập nghiệm của bất phương trình \({\log _{\frac{1}{2}}}\left( {3x - 2} \right) > {\log _{\frac{1}{2}}}\left( {4 - x} \right)\) là
Đáp án C
Phương pháp giải:
Giải bất phương trình dạng \({\log _a}f\left( x \right) > {\log _a}g\left( x \right) \Leftrightarrow 0 < f\left( x \right) < g\left( x \right)\) (với \(0 < a < 1\)).
Giải chi tiết:
Ta có: \({\log _{\frac{1}{2}}}\left( {3x - 2} \right) > {\log _{\frac{1}{2}}}\left( {4 - x} \right)\)
\( \Leftrightarrow 0 < 3x - 2 < 4 - x \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{3x - 2 > 0}\\{4x < 6}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x > \frac{2}{3}}\\{x < \frac{3}{2}}\end{array}} \right.\)
Vậy tập nghiệm của bất phương trình \(S = \left( {\frac{2}{3};\frac{3}{2}} \right)\).Câu 16:
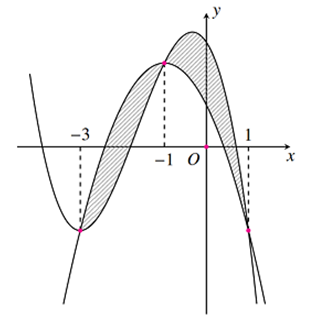
Hình bên vẽ đồ thị các hàm số \(f\left( x \right) = - {x^2} - 2x + 1\) và \[g\left( x \right) = - \frac{1}{2}{x^3} - \frac{5}{2}{x^2} - \frac{3}{2}x + \frac{5}{2}\]. Diện tích phần gạch chép trong hình bằng
Đáp án A
Phương pháp giải:
Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số \[y = f(x),{\mkern 1mu} {\mkern 1mu} y = g(x)\], trục hoành và hai đường thẳng \[x = a;{\mkern 1mu} {\mkern 1mu} x = b\] được tính theo công thức : \[S = \int\limits_a^b {\left| {f(x) - g(x)} \right|dx} \].
Giải chi tiết:
Dựa vào đồ thị hàm số ta thấy: \(f\left( x \right) = g\left( x \right) \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = - 3}\\{x = - 1}\\{x = 1}\end{array}} \right.\)
Diện tích phần gạch chép trong hình bằng: \(S = \int\limits_{ - 3}^1 {\left| {f\left( x \right) - g\left( x \right)} \right|} {\mkern 1mu} dx\)
\( = \int\limits_{ - 3}^{ - 1} {\left[ {f\left( x \right) - g\left( x \right)} \right]} {\mkern 1mu} dx + \int\limits_{ - 1}^1 {\left[ {g\left( x \right) - f\left( x \right)} \right]} {\mkern 1mu} dx\).
Câu 17:
Cho hàm số \(y = \frac{{mx - 18}}{{x - 2m}}\). Gọi \(S\) là tập hợp các giá trị nguyên của tham số \(m\)để hàm số đồng biến trên khoảng \(\left( {2; + \infty } \right)\). Tổng các phần tử của \(S\) bằng:
Đáp án A
Phương pháp giải:
- Tìm TXĐ \(D = \mathbb{R}\backslash \left\{ {{x_0}} \right\}\)
- Để hàm số đồng biến trên \(\left( {a;b} \right)\) thì \(y' > 0{\mkern 1mu} {\mkern 1mu} \forall x \in \left( {a;b} \right) \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{y' > 0}\\{{x_0} \notin \left( {a;b} \right)}\end{array}} \right.\).
Giải chi tiết:
TXĐ: \(D = \mathbb{R}\backslash \left\{ {2m} \right\}\)
Ta có: \(y = \frac{{mx - 18}}{{x - 2m}} \Rightarrow y' = \frac{{ - 2{m^2} + 18}}{{{{\left( {x - 2m} \right)}^2}}}\)
Để hàm số đồng biến trên khoảng \(\left( {2; + \infty } \right)\) thì \(y' > 0{\mkern 1mu} {\mkern 1mu} \forall x \in \left( {2; + \infty } \right)\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{18 - 2{m^2} > 0}\\{2m \notin \left( {2; + \infty } \right)}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{ - 3 < m < 3}\\{2m \le 2}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{ - 3 < m < 3}\\{m \le 1}\end{array}} \right. \Leftrightarrow - 3 < m \le 1\)
Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 2; - 1;0;1} \right\} = S\).
Vậy tổng các phần tử của \(S\) bằng: \( - 2 - 1 + 0 + 1 = - 2\).
Câu 18:
Biết \(z = a + bi{\mkern 1mu} {\mkern 1mu} \left( {a,b \in \mathbb{R}} \right)\) là nghiệm của phương trình \(\left( {1 + 2i} \right)z + \left( {3 - 4i} \right)\bar z = - 42 - 54i\). Khi đó \(a + b\) bằng
Đáp án A
Phương pháp giải:
- Đặt \(z = a + bi \Rightarrow \bar z = a - bi\). Thay vào phương trình.
- Sử dụng điều kiện để hai số phức bằng nhau.
Giải chi tiết:
Ta có \(z = a + bi \Rightarrow \bar z = a - bi\)
Khi đó: \(\left( {1 + 2i} \right)z + \left( {3 - 4i} \right)\bar z = - 42 - 54i\)
\( \Leftrightarrow \left( {1 + 2i} \right)\left( {a + bi} \right) + \left( {3 - 4i} \right)\left( {a - bi} \right) = - 42 - 54i\)
\( \Leftrightarrow \left( {4a - 6b} \right) + \left( { - 2a - 2b} \right)i = - 42 - 54i\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{4a - 6b = - 42}\\{ - 2a - 2b = - 54}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 12}\\{b = 15}\end{array}} \right.\)
\( \Rightarrow a + b = 27\).Câu 19:
Tập hợp các điểm biểu diễn các số phức \(z\) thỏa mãn \(\left| {z + i - 1} \right| = \left| {\bar z - 2i} \right|\) là:
Đáp án A
Phương pháp giải:
- Đặt \(z = x + yi \Rightarrow \bar z = x - yi\)
- Thay \[z,{\mkern 1mu} {\mkern 1mu} \bar z\] vào phương trình đề bài cho.
- Sử dụng công thức \[\left| {a + bi} \right| = \sqrt {{a^2} + {b^2}} \].
- Bình phương hai vế, tìm mối quan hệ giữa \[x,{\mkern 1mu} {\mkern 1mu} y\] và kết luận.
Giải chi tiết:
Đặt \[z = x + yi \Rightarrow \bar z = x - yi\]. Theo bài ra ta có:
\[\left| {z + i - 1} \right| = \left| {\bar z - 2i} \right|\]
\[ \Leftrightarrow \left| {x + yi + i - 1} \right| = \left| {x - yi - 2z} \right|\]
\[ \Leftrightarrow \left| {x - 1 + \left( {y + 1} \right)i} \right| = \left| {x - \left( {y + 2} \right)i} \right|\]
\[ \Leftrightarrow {\left( {x - 1} \right)^2} + {\left( {y + 1} \right)^2} = {x^2} + {\left( {y + 2} \right)^2}\]
\[ \Leftrightarrow {x^2} - 2x + 1 + {y^2} + 2y + 1 = {x^2} + {y^2} + 4y + 4\]
\[ \Leftrightarrow 2x + 2y + 2 = 0\]
\[ \Leftrightarrow x + y + 1 = 0\]
Vậy tập hợp các điểm biểu diễn số phức \[z\] là đường thẳng có phương trình \[x + y + 1 = 0\].
Câu 20:
Trong mặt phẳng với hệ tọa độ \[Oxy,\] cho hình vuông \[ABCD\] có diện tích bằng 10 và \[A \in d:x - y - 2 = 0,{\mkern 1mu} {\mkern 1mu} CD:3x - y = 0.\] Với \({x_C} > 0\), số điểm \(C\) tìm được là
Đáp án C
Phương pháp giải:
Tham số hóa điểm \(A\)sau đó sử dụng công thức diện tích tìm \(A\). Viết phương trình \(CD\) và tính được \(D\).
Tham số hóa điểm \(C\) và dựa vào khoảng cách \(CD\) để tìm \(C\).
Giải chi tiết:
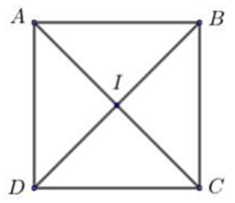
\(A \in d:x - y - 2 = 0 \Rightarrow A\left( {t;t - 2} \right)\)
\(S = A{D^2} = 10 \Rightarrow AD = \sqrt {10} \)
\( \Rightarrow d\left( {A,CD} \right) = AD = \frac{{\left| {3t - t + 2} \right|}}{{\sqrt {10} }} = \sqrt {10} \)
\( \Leftrightarrow \left| {2t + 2} \right| = 10 \Leftrightarrow \left| {t + 1} \right| = 5 \Rightarrow \left[ {\begin{array}{*{20}{l}}{t = 4}\\{t = - 6}\end{array}} \right. \Rightarrow \left[ {\begin{array}{*{20}{l}}{A\left( {4;2} \right)}\\{A\left( { - 6; - 8} \right)}\end{array}} \right.\)
TH1: \(A\left( {4;2} \right) \Rightarrow AD\left\{ {\begin{array}{*{20}{l}}{qua{\mkern 1mu} {\mkern 1mu} A\left( {4;2} \right)}\\{ \bot CD:3x - y = 0}\end{array}} \right. \Rightarrow AD:x + 3y - 10 = 0\)
\(D = AD \cap CD \Rightarrow D:\left\{ {\begin{array}{*{20}{l}}{x + 3y - 10 = 0}\\{3x - y = 0}\end{array}} \right. \Rightarrow D\left( {1;3} \right)\)
\(C \in CD:3x - y = 0 \Rightarrow C\left( {c;3c} \right)\)
\(CD = \sqrt {10} \Rightarrow {\left( {c - 1} \right)^2} + {\left( {3c - 3} \right)^2} = 10 \Rightarrow \left[ {\begin{array}{*{20}{l}}{c = 2}\\{c = 0}\end{array}} \right. \Rightarrow \left[ {\begin{array}{*{20}{l}}{C\left( {2;6} \right)}\\{C\left( {0;0} \right)}\end{array}} \right.\)
TH2: \(A\left( { - 6; - 8} \right) \Rightarrow AD:x + 3y + 30 = 0\)
\( \Rightarrow D\left( { - 3; - 9} \right)\)
\(C\left( {c;3c} \right) \Rightarrow {\left( {c + 3} \right)^2} + {\left( {3c + 9} \right)^2} = 10 \Rightarrow \left[ {\begin{array}{*{20}{l}}{c = - 2}\\{c = - 4}\end{array}} \right. \Rightarrow \left[ {\begin{array}{*{20}{l}}{C\left( { - 2; - 6} \right)}\\{C\left( { - 4; - 12} \right)}\end{array}} \right.\).
Câu 21:
Cho hai đường tròn \(\left( {{C_1}} \right):{\mkern 1mu} {\mkern 1mu} {x^2} + {y^2} = 4\) và \[\left( {{C_2}} \right):{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {x^2} + {y^2} - 2\left( {2m - 1} \right)x - 2\left( {m - 2} \right)y + m + 6 = 0.\] Xác định \[m\] để hai đường tròn trên tiếp xúc ngoài với nhau.
Đáp án B
Phương pháp giải:
Đường tròn \[\left( {{C_1}} \right)\] có tâm \[{I_1},\] bán kính \({R_1}\) tiếp xúc ngoài với đường tròn \(\left( {{C_2}} \right)\) có tâm \({I_2},\) bán kính \({R_2}\) \( \Rightarrow {I_1}{I_2} = {R_1} + {R_2}.\)
Giải chi tiết:
Để phương trình \(\left( {{C_2}} \right)\) là phương trình đường tròn thì: \({\left( {2m - 1} \right)^2} + {\left( {m - 2} \right)^2} - m - 6 > 0\)
\( \Leftrightarrow 4{m^2} - 4m + 1 + {m^2} - 4m + 4 - m - 6 > 0\)
\( \Leftrightarrow 5{m^2} - 9m - 1 > 0{\mkern 1mu} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m > \frac{{9 + \sqrt {101} }}{{10}}}\\{m < \frac{{9 - \sqrt {101} }}{{10}}}\end{array}} \right.\)
\( \Rightarrow \left( {{C_2}} \right)\) luôn là phương trình đường tròn với \(\left[ {\begin{array}{*{20}{l}}{m > \frac{{9 + \sqrt {101} }}{{10}}}\\{m < \frac{{9 - \sqrt {101} }}{{10}}}\end{array}} \right..\)
Ta có: \(\left( {{C_1}} \right)\) có tâm \({I_1}\left( {0;{\mkern 1mu} {\mkern 1mu} 0} \right)\) và bán kính \({R_1} = 2\).
\(\left( {{C_2}} \right)\) có tâm \({I_2}\left( {2m - 1;{\mkern 1mu} {\mkern 1mu} m - 2} \right)\) và bán kính \({R_2} = \sqrt {{{\left( {2m - 1} \right)}^2} + {{\left( {m - 2} \right)}^2} - m - 6} = \sqrt {5{m^2} - 9m - 1} .\)
Đường tròn \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right)\) tiếp xúc ngoài với nhau \( \Leftrightarrow {I_1}{I_2} = {R_1} + {R_2}\)
\( \Leftrightarrow \sqrt {{{\left( {2m - 1} \right)}^2} + {{\left( {m - 2} \right)}^2}} = 2 + \sqrt {5{m^2} - 9m - 1} \)
\( \Leftrightarrow \sqrt {5{m^2} - 8m + 5} = 2 + \sqrt {5{m^2} - 9m - 1} \)
\( \Leftrightarrow 5{m^2} - 8m + 5 = 4 + 4\sqrt {5{m^2} - 9m - 1} + 5{m^2} - 9m - 1\)
\( \Leftrightarrow m + 2 = 4\sqrt {5{m^2} - 9m - 1} \)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m + 2 \ge 0}\\{{{\left( {m + 2} \right)}^2} = 16\left( {5{m^2} - 9m - 1} \right)}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m \ge - 2}\\{{m^2} + 4m + 4 = 80{m^2} - 144m - 16}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m \ge - 2}\\{79{m^2} - 148m - 20 = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m \ge - 2}\\{\left[ {\begin{array}{*{20}{l}}{m = 2}\\{m = - \frac{{10}}{{79}}}\end{array}} \right.}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m = 2}\\{m = - \frac{{10}}{{79}}}\end{array}} \right.\)
Đối chiếu với điều kiện chỉ có \(m = 2\) thỏa mãn yêu cầu bài toán.Câu 22:
Trong không gian \(Oxyz\), viết phương trình của mặt phẳng \(\left( P \right)\) biết \(\left( P \right)\) đi qua hai điểm \(M\left( {0; - 1;0} \right),{\mkern 1mu} {\mkern 1mu} N\left( { - 1;1;1} \right)\) và vuông góc với mặt phẳng \(\left( {Oxz} \right)\).
Đáp án D
Phương pháp giải:
+) \(\left\{ {\begin{array}{*{20}{l}}{\left( P \right) \supset MN \Rightarrow \overrightarrow {{n_P}} .\overrightarrow {MN} = 0}\\{\left( P \right) \bot \left( {Oxz} \right) \Rightarrow \vec n.\vec j = 0}\end{array}} \right. \Rightarrow \vec n = \left[ {\overrightarrow {MN} ;\vec j} \right]\)
+) Mặt phẳng \(\left( P \right)\) đi qua \(M\left( {{x_0};{y_0};{z_0}} \right)\) và có 1 VTPT \(\vec n\left( {A;B;C} \right)\) có phương trình
\(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0\).
Giải chi tiết:
Gọi \(\vec n\) là 1 VTPT của \(\left( P \right)\).
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{\left( P \right) \supset MN \Rightarrow \overrightarrow {{n_P}} .\overrightarrow {MN} = 0}\\{\left( P \right) \bot \left( {Oxz} \right) \Rightarrow \vec n.\vec j = 0}\end{array}} \right. \Rightarrow \vec n = \left[ {\overrightarrow {MN} ;\vec j} \right]\) với \(\overrightarrow {MN} = \left( { - 1;2;1} \right);{\mkern 1mu} {\mkern 1mu} \vec j = \left( {0;1;0} \right)\)
\( \Rightarrow \vec n = \left( { - 1;0; - 1} \right)//\left( {1;0;1} \right)\).
Vậy phương trình mặt phẳng \(\left( P \right)\) là \(1\left( {x - 0} \right) + 1\left( {z - 0} \right) = 0 \Leftrightarrow x + z = 0\).
Câu 23:
Cho hình nón có góc ở đỉnh bằng \({120^0}\) và đường cao bằng 2. Tính diện tích xung quanh của hình nón đã cho.
Đáp án B
Phương pháp giải:
- Sử dụng tính chất tam giác cân: Đường trung tuyến đồng thời là đường phân giác.
- Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông tính độ dài đường sinh \(l\) và bán kính đáy \(r\) của hình nón.
- Áp dụng công thức tính diện tích xung quanh của hình nón có độ dài đường sinh \(l\) và bán kính đáy \(r\) là \({S_{xq}} = \pi rl\).
Giải chi tiết:
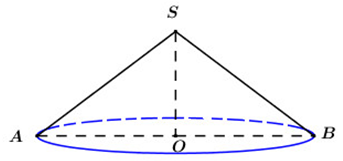
Gọi \(S\) là đỉnh hình nón, \(AB\) là 1 đường kính của hình nón và \(O\) là tâm đường tròn đáy của hình nón.
Khi đó ta có \(\angle ASB = {120^0}\) và \(h = SO = 2\).
Ta có: \(\Delta SAB\) cân tại \(S\) suy ra \(SO\) là phân giác của \(\angle ASB\).
\( \Rightarrow \angle ASO = \frac{1}{2}\angle ASB = {60^0}\)
Xét tam giác vuông \(SOA\) có: \(r = OA = SO.\tan {60^0} = 2\sqrt 3 \), \(l = SA = \frac{{SO}}{{\cos {{60}^0}}} = 4\)
Vậy diện tích xung quanh của hình nón là: \({S_{xq}} = \pi rl = \pi .2\sqrt 3 .4 = 8\sqrt 3 \pi \).
Câu 24:
Một que kem ốc quế gồm hai phần : phần kem có dạng hình cầu, phần ốc quế có dạng hình nón. Giả sử hình cầu và hình nón cùng có bán kính bằng \(3{\mkern 1mu} cm,\) chiều cao hình nón là \(9cm.\) Thể tích của que kem (bao gồm cả phần không gian bên trong ốc quế không chứa kem) có giá trị bằng:
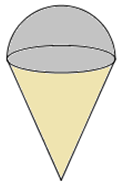
Đáp án A
Phương pháp giải:
Công thức tính thể tích của khối nón có bán kính đáy R và chiều cao h là: \(V = \frac{1}{3}\pi {R^2}h.\)
Công thức tính thể của khối cầu có bán kính R là: \(V = \frac{4}{3}\pi {R^3}.\)
Giải chi tiết:
Ta có thể tích của phần kem là: \({V_1} = \frac{1}{2}.\frac{4}{3}.\pi {R^3}\)\( = \frac{2}{3}\pi {.3^3} = 18\pi {\mkern 1mu} {\mkern 1mu} c{m^3}.\)
Thể tích của phần ốc quế bên dưới là: \({V_2} = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi {.3^2}.9 = 27\pi {\mkern 1mu} {\mkern 1mu} c{m^3}.\)
Vậy \(V = {V_1} + {V_2} = 18\pi + 27\pi = 45\pi {\mkern 1mu} {\mkern 1mu} c{m^3}.\)
Câu 25:
Cho hình lăng trụ \(ABC.A'B'C'\) có \(AA' = 2\sqrt {13} a\), tam giác \(ABC\) vuông tại \(C\) và \(\angle ABC = {30^0}\), góc giữa cạnh bên \(CC'\) và mặt đáy \(\left( {ABC} \right)\) bằng \({60^0}\). Hình chiếu vuông góc của \(B'\) lên mặt phẳng \(\left( {ABC} \right)\) trùng với trọng tâm của tam giác \(ABC\). Thể tích của khối tứ diện \(A'ABC\) theo \(a\) bằng:
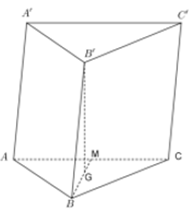
Đáp án B
Phương pháp giải:
- Chứng minh \(\angle \left( {CC';\left( {ABC} \right)} \right) = \angle \left( {BB';\left( {ABC} \right)} \right) = {60^0}\), , xác định góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đó.
- Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông tính \(B'G,{\mkern 1mu} {\mkern 1mu} BM\) (M là trung điểm của \(AC\)).
- Đặt \(BC = x\), tính \(MC\) theo x.
- Áp dụng định lí Pytago trong tam giác vuông \(BCM\) tìm x theo a.
- Tính \({V_{A'ABC}} = \frac{1}{3}.B'G.{S_{\Delta ABC}}\).
Giải chi tiết:
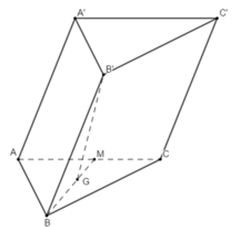
Ta có \(CC'//BB' \Rightarrow \angle \left( {CC';\left( {ABC} \right)} \right) = \angle \left( {BB';\left( {ABC} \right)} \right) = {60^0}\)
Vì \(B'G \bot \left( {ABC} \right)\) nên \(GB\) là hình chiếu vuông góc của \(B'B\) lên \(\left( {ABC} \right)\).
\( \Rightarrow \angle \left( {BB';\left( {ABC} \right)} \right) = \angle \left( {BB';BG} \right) = \angle B'BG = {60^0}\)
Xét tam giác vuông \(BB'G\) ta có: \(BB' = AA' = 2\sqrt {13} a\)
\( \Rightarrow B'G = BB'.\sin {60^0} = a\sqrt {39} \) và \(BG = BB'.\cos {60^0} = a\sqrt {13} \)
\( \Rightarrow BM = \frac{3}{2}BG = \frac{{3a\sqrt {13} }}{2}\)
Đặt \(BC = x \Rightarrow AC = BC.\tan {30^0} = \frac{{x\sqrt 3 }}{3} \Rightarrow MC = \frac{1}{2}AC = \frac{{x\sqrt 3 }}{6}\)
Áp dụng định lí Pytago trong tam giác vuông \(BMC\) ta có:
\(B{M^2} = M{C^2} + B{C^2}\)
\( \Leftrightarrow {\left( {\frac{{3a\sqrt {13} }}{2}} \right)^2} = {\left( {\frac{{x\sqrt 3 }}{6}} \right)^2} + {x^2}\)
\( \Leftrightarrow \frac{{117{a^2}}}{4} = \frac{{13{x^2}}}{{12}}\)
\( \Leftrightarrow {x^2} = 27{a^2} \Rightarrow x = 3a\sqrt 3 = BC\)
\( \Rightarrow AC = 3a\).
Nên \( \Rightarrow {S_{\Delta ABC}} = \frac{1}{2}.AC.BC = \frac{1}{2}.3a.3a\sqrt 3 = \frac{{9{a^2}\sqrt 3 }}{2}\)
Vậy \({V_{A'ABC}} = \frac{1}{3}.B'G.{S_{\Delta ABC}} = \frac{1}{3}.a\sqrt {39} .\frac{{9{a^2}\sqrt 3 }}{2} = \frac{{9{a^3}\sqrt {13} }}{2}\).
Câu 26:
Cho tứ diện \(ABCD\) có \(AC = a,{\mkern 1mu} {\mkern 1mu} BD = 3a\). Gọi \(M\) và \(N\) lần lượt là trung điểm của \(AD\) và \(BC.\) Biết \(AC\) vuông góc với \(BD\). Tính độ dài đoạn thẳng \(MN\) theo \(a\).
Đáp án C
Phương pháp giải:
- Gọi \(P\) là trung điểm của \(AB\). Tính \(PM,{\mkern 1mu} {\mkern 1mu} PN\).
- Chứng minh \(\Delta PMN\) vuông, áp dụng định lí Pytago tính \[MN\].
Giải chi tiết: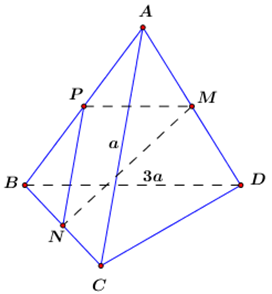
Gọi \[P\] là trung điểm của \[AB\].
Ta có: \[PM,{\mkern 1mu} {\mkern 1mu} PN\] lần lượt là đường trung bình của \[\Delta ACD,{\mkern 1mu} {\mkern 1mu} \Delta ABC\] nên \[PM = \frac{1}{2}BD = \frac{{3a}}{2}\], \[PN = \frac{1}{2}AC = \frac{a}{2}\] và \[\left\{ {\begin{array}{*{20}{l}}{PM\parallel BD}\\{PN\parallel AC}\end{array}} \right.\].
Mà \[AC \bot BD{\mkern 1mu} {\mkern 1mu} \left( {gt} \right)\] nên \[PM \bot PN\], do đó tam giác \[PMN\] vuông tại \[P\].
Áp dụng định lí Pytago ta có: \[MN = \sqrt {P{M^2} + P{N^2}} \]\[ = \sqrt {\frac{{9{a^2}}}{4} + \frac{{{a^2}}}{4}} = \frac{{a\sqrt {10} }}{2}\].
Câu 27:
Trong không gian cho hai điểm \[A,B\] cố định và độ dài đoạn thẳng \[AB\] bằng 4. Biết rằng tập hợp các điểm \[M\] sao cho \[MA = 3MB\] là một mặt cầu. Tìm bán kính \[R\] của mặt cầu đó?
Đáp án C
Giải chi tiết:
Gọi \(I\) là điểm thỏa mãn \(\overrightarrow {IA} = 9\overrightarrow {IB} \)
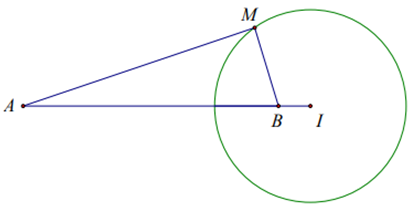
\(MA = 3MB \Leftrightarrow M{A^2} = 9M{B^2}\)
\( \Leftrightarrow {\left( {\overrightarrow {MI} + \overrightarrow {IA} } \right)^2} = 9{\left( {\overrightarrow {MI} + \overrightarrow {IA} } \right)^2}\)
\( \Leftrightarrow {\overrightarrow {MI} ^2} + 2\overrightarrow {MI} .\overrightarrow {IA} + {\overrightarrow {IA} ^2} = 9{\overrightarrow {MI} ^2} + 18\overrightarrow {MI} .\overrightarrow {IB} + 9{\overrightarrow {IB} ^2}\)
\( \Leftrightarrow - 8M{I^2} + 2\overrightarrow {MI} \left( {\overrightarrow {IA} - 9\overrightarrow {IB} } \right) = 9I{B^2} - I{A^2}\)
\( \Leftrightarrow M{I^2} = \frac{{I{A^2} - 9I{B^2}}}{8}\)
Dễ dàng tính được \(IA = \frac{9}{8}AB = \frac{9}{2}{\mkern 1mu} ;{\mkern 1mu} {\mkern 1mu} IB = \frac{1}{8}AB = \frac{1}{2}\)
\( \Rightarrow R = MI = \sqrt {\frac{{I{A^2} - 9I{B^2}}}{8}} = \sqrt {\frac{{{{\left( {\frac{9}{2}} \right)}^2} - {{\left( {\frac{1}{2}} \right)}^2}}}{8}} = \frac{3}{2}\).
Câu 28:
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( P \right):{\mkern 1mu} {\mkern 1mu} 3x - y + z - 7 = 0\). Phương trình đường thẳng \(\Delta \) đi qua điểm \(A\left( {2; - 3;1} \right)\) và vuông góc với mặt phẳng \(\left( P \right)\) là:
Đáp án D
Phương pháp giải:
- \[d \bot \left( P \right) \Rightarrow \overrightarrow {{u_d}} = \overrightarrow {{n_P}} \]
- Đường thẳng đi qua \[M\left( {{x_0};{y_0};{z_0}} \right)\] và có 1 VTCP \[\vec u\left( {a;b;c} \right)\] có phương trình tham số \[\left\{ {\begin{array}{*{20}{l}}{x = {x_0} + at}\\{y = {y_0} + bt}\\{z = {z_0} + ct}\end{array}} \right.\].
Giải chi tiết:
Mặt phẳng \[\left( P \right):{\mkern 1mu} {\mkern 1mu} 3x - y + z - 7 = 0\] có 1 VTPT \[\overrightarrow {{n_P}} = \left( {3; - 1;1} \right)\].
Vì đường thẳng \[\Delta \] vuông góc với mặt phẳng \[\left( P \right)\] nên có 1 VTCP là \(\overrightarrow {{u_\Delta }} = \overrightarrow {{n_P}} = \left( {3; - 1;1} \right)\).
Vậy phương trình tham số của đường thẳng Δ là: \(\left\{ {\begin{array}{*{20}{l}}{x = 2 + 3t}\\{y = - 3 - t}\\{z = 1 + t}\end{array}} \right.\).
Câu 29:
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {\left( {x + 1} \right)^2}\left( {x - 3} \right)\). Tìm số điểm cực trị của hàm số \(g\left( x \right) = f\left( {\sqrt {{x^2} + 2x + 6} } \right)\).
Đáp án C
Phương pháp giải:
- Từ \(f'\left( x \right)\) suy ra các nghiệm của phương trình \(f'\left( x \right) = 0\), chú ý nghiệm bội chẵn, bội lẻ.
- Tính đạo hàm \(g'\left( x \right)\).
- Giải phương trình \(g'\left( x \right) = 0\) xác định các nghiệm bội lẻ.
Giải chi tiết:
Theo bài ra ta có: \(f'\left( x \right) = 0 \Leftrightarrow {\left( {x + 1} \right)^2}\left( {x - 3} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = - 1{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {nghiem{\mkern 1mu} {\mkern 1mu} boi{\mkern 1mu} {\mkern 1mu} 2} \right)}\\{x = 3{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {nghiem{\mkern 1mu} {\mkern 1mu} don} \right)}\end{array}} \right.\)
Ta có: \(g\left( x \right) = f\left( {\sqrt {{x^2} + 2x + 6} } \right)\)
\( \Rightarrow g'\left( x \right) = \frac{{2x + 2}}{{2\sqrt {{x^2} + 2x + 6} }}f'\left( {\sqrt {{x^2} + 2x + 6} } \right)\)
\({\mkern 1mu} = \frac{{x + 1}}{{\sqrt {{x^2} + 2x + 6} }}f'\left( {\sqrt {{x^2} + 2x + 6} } \right)\)
Cho \(g'\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x + 1 = 0}\\{f'\left( {\sqrt {{x^2} + 2x + 6} } \right) = 0}\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = - 1}\\{\sqrt {{x^2} + 2x + 6} = 3}\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = - 1}\\{{x^2} + 2x + 6 = 9}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = - 1}\\{{x^2} + 2x - 3 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = - 1}\\{x = 1}\\{x = - 3}\end{array}} \right.\) (đều là các nghiệm đơn).
(Ta không xét \(\sqrt {{x^2} + 2x + 6} = - 1\) vì \(f'\left( x \right)\) không đổi dấu qua \(x = - 1\) nên nghiệm của phương trình \(\sqrt {{x^2} + 2x + 6} = - 1\) không làm cho \(g'\left( x \right)\) đổi dấu).
Vậy hàm số đã cho có 3 điểm cực trị.
Câu 30:
Trong không gian với hệ tọa độ \(Oxyz\) cho \(A\left( {0;1;0} \right)\), \(B\left( {2;2;2} \right)\), \(C\left( { - 2;3;1} \right)\) và đường thẳng \(d:{\mkern 1mu} {\mkern 1mu} \frac{{x - 1}}{2} = \frac{{y + 2}}{{ - 1}} = \frac{{z - 3}}{2}\). Tìm điểm \(M \in d\) sao cho thể tích tứ diện \(MABC\) bằng 3.
Đáp án A
Phương pháp giải:
Sử dụng công thức: \({V_{ABCD}} = \frac{1}{6}\left| {\left[ {\overrightarrow {AB} ;\overrightarrow {AC} } \right].\overrightarrow {AM} } \right|\)
Giải chi tiết:
Giả sử \(M\left( {a;b;c} \right) \in d\) ta có:
\(\frac{{a - 1}}{2} = \frac{{b + 2}}{{ - 1}} = \frac{{c - 3}}{2} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{ - a + 1 = 2b + 4}\\{2b + 4 = - c + 3}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = - 2b - 3}\\{c = - 2b - 1}\end{array}} \right.\)
\( \Rightarrow M\left( { - 2b - 3;b; - 2b - 1} \right)\)
Ta có: \(\overrightarrow {AB} = \left( {2;1;2} \right);{\mkern 1mu} {\mkern 1mu} \overrightarrow {AC} = \left( { - 2;2;1} \right)\); \(\overrightarrow {AM} = \left( {a;b - 1;c} \right) = \left( { - 2b - 3;b - 1; - 2b - 1} \right)\).
\(\left[ {\overrightarrow {AB} ;\overrightarrow {AC} } \right] = \left( { - 3; - 6;6} \right)\)
\(\left[ {\overrightarrow {AB} ;\overrightarrow {AC} } \right].\overrightarrow {AM} = - 3.\left( { - 2b - 3} \right) - 6\left( {b - 1} \right) + 6\left( { - 2b - 1} \right)\)\( = - 12b + 9\)
\( \Rightarrow {V_{ABCD}} = \frac{1}{6}\left| {\left[ {\overrightarrow {AB} ;\overrightarrow {AC} } \right].\overrightarrow {AM} } \right| = \frac{1}{6}\left| {12b - 9} \right| = \frac{1}{2}\left| {4b - 3} \right|\)
Theo bài ra ta có: \(\frac{1}{2}\left| {4b - 3} \right| = 3 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{b = \frac{9}{4}}\\{b = - \frac{3}{4}}\end{array}} \right. \Rightarrow \left[ {\begin{array}{*{20}{l}}{M\left( { - \frac{{15}}{2};\frac{9}{4}; - \frac{{11}}{2}} \right)}\\{M\left( { - \frac{3}{2}; - \frac{3}{4};\frac{1}{2}} \right)}\end{array}} \right.\).
Câu 31:
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {\left( {x - 1} \right)^3}\left[ {{x^2} + \left( {4m - 5} \right)x + {m^2} - 7m + 6} \right],{\mkern 1mu} {\mkern 1mu} \forall x \in \mathbb{R}\). Có bao nhiêu số nguyên m để hàm số \(g\left( x \right) = f\left( {\left| x \right|} \right)\) có đúng 5 điểm cực trị?
Đáp án A
Phương pháp giải:
Nếu hàm số \(y = f\left( x \right)\) có n điểm cực trị dương thì hàm số \(y = f\left( {\left| x \right|} \right)\) có \(n + 1\) điểm cực trị.
Giải chi tiết:
Để hàm số \(g\left( x \right) = f\left( {\left| x \right|} \right)\) có đúng 5 điểm cực trị thì hàm số \(y = f\left( x \right)\) phải có 2 điểm cực trị dương \( \Rightarrow \) Phương trình \(f'\left( x \right) = 0\) phải có 2 nghiệm bội lẻ dương phân biệt.
Xét \(f'\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {nghiem{\mkern 1mu} {\mkern 1mu} boi{\mkern 1mu} {\mkern 1mu} 3} \right)}\\{{x^2} + \left( {4m - 5} \right)x + {m^2} - 7m + 6 = 0{\mkern 1mu} {\mkern 1mu} \left( * \right)}\end{array}} \right.\)
Do đó phương trình (*) cần phải có 1 nghiệm bội lẻ dương khác 1.
Ta có: \(\Delta = {\left( {4m - 5} \right)^2} - 4\left( {{m^2} - 7m + 6} \right)\)
\( = 16{m^2} - 40m + 25 - 4{m^2} + 28m - 24\)
\( = 12{m^2} - 12m + 1\)
Để (*) có 1 nghiệm bội lẻ dương khác 1 thì:
\(\left\{ {\begin{array}{*{20}{l}}{\Delta = 12{m^2} - 12m + 1 > 0}\\{P = {m^2} - 7m + 6 \le 0}\\{1 + 4m - 5 + {m^2} - 7m + 6 \ne 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\left[ {\begin{array}{*{20}{l}}{m > \frac{{3 + \sqrt 6 }}{6}}\\{m < \frac{{3 - \sqrt 6 }}{6}}\end{array}} \right.}\\{1 \le m \le 6}\\{m \ne 1}\\{m \ne 2}\end{array}} \right.\)\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{1 < m \le 6}\\{m \ne 2}\end{array}} \right.\)
Vậy có 4 số nguyên m thỏa mãn yêu cầu bài toán.
Câu 32:
Tìm \(m\) để phương trình \(2x - 4 = 3\sqrt {x - m} \) có nghiệm.
Đáp án A
Phương pháp giải:
Giải phương trình dạng \(\sqrt A = B \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{A \ge 0}\\{A = {B^2}}\end{array}} \right.\).
Giải chi tiết:
ĐKXĐ: \(x - m \ge 0 \Leftrightarrow x \ge m\)
Ta có: \(2x - 4 = 3\sqrt {x - m} \)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \ge 2}\\{4{{\left( {x - 2} \right)}^2} = 9\left( {x - m} \right)}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \ge 2}\\{4{x^2} - 16x + 16 = 9x - 9m}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \ge 2}\\{4{x^2} - 25x + 9m + 16 = 0{\mkern 1mu} {\mkern 1mu} \left( * \right)}\end{array}} \right.\)
Để phương trình ban đầu có nghiệm thì phương trình (*) phải có nghiệm \(x \ge 2\).
\( \Rightarrow \Delta = {25^2} - 4.4\left( {9m + 16} \right) \ge 0\)
\( \Leftrightarrow 369 - 144m \ge 0 \Leftrightarrow m \le \frac{{41}}{{16}}\)
Khi đó phương trình có 2 nghiệm \(x = \frac{{25 \pm \sqrt {369 - 144m} }}{8}\)
\( \Rightarrow \left[ {\begin{array}{*{20}{l}}{\frac{{25 + \sqrt {369 - 144m} }}{8} \ge 2}\\{\frac{{25 - \sqrt {369 - 144m} }}{8} \ge 2}\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\sqrt {369 - 144m} \ge - 9{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {luon{\mkern 1mu} {\mkern 1mu} dung} \right)}\\{\sqrt {369 - 144m} \le 9}\end{array}} \right.\)
\( \Leftrightarrow 0 \le 369 - 144m \le 81\)
\( \Leftrightarrow 2 \le m \le \frac{{41}}{{16}}\).
Kết hợp điều kiện \(\left\{ {\begin{array}{*{20}{l}}{x \ge 2}\\{x \ge m}\end{array}} \right.\) ta thấy \(2 \le m \le \frac{{41}}{{16}}\) thỏa mãn.
Vậy \(2 \le m \le \frac{{41}}{{16}}\).
Câu 33:
Cho hàm số \(y = f\left( x \right)\) liên tục trên tập số thực thỏa mãn \(f\left( x \right) + \left( {5x - 2} \right)f\left( {5{x^2} - 4x} \right)\) \( = 50{x^3} - 60{x^2} + 23x - 1\) \(\forall x \in \mathbb{R}\). Giá trị của biểu thức \(\int\limits_0^1 {f\left( x \right)dx} \) bằng:
Đáp án A
Phương pháp giải:
- Lấy tích phân từ 0 đến 1 hai vế.
- Sử dụng phương pháp đổi biến số.
- Sử dụng tính chất tích phân: \(\int\limits_a^b {f\left( x \right)dx} = \int\limits_a^b {f\left( t \right)dt} \).
Giải chi tiết:
Lấy tích phân từ 0 đến 1 hai vế ta được:
\(\int\limits_0^1 {f\left( x \right)dx} + \int\limits_0^1 {\left( {5x - 2} \right)f\left( {5{x^2} - 4x} \right)dx} = \int\limits_0^1 {\left( {50{x^3} - 60{x^2} + 23x - 1} \right)dx} \)
Xét tích phân \(I = \int\limits_0^1 {\left( {5x - 2} \right)f\left( {5{x^2} - 4x} \right)dx} \).
Đặt \(t = 5{x^2} - 4x\) ta có: \(dt = \left( {10x - 4} \right)dx \Leftrightarrow \left( {5x - 2} \right)dx = \frac{1}{2}dt\)
Đổi cận: \(\left\{ {\begin{array}{*{20}{l}}{x = 0 \Rightarrow t = 0}\\{x = 1 \Rightarrow t = 1}\end{array}} \right.\)
\( \Rightarrow I = \int\limits_0^1 {\frac{1}{2}f\left( t \right)dt} = \frac{1}{2}\int\limits_0^1 {f\left( x \right)dx} \)
Xét tích phân \(J = \int\limits_0^1 {\left( {50{x^3} - 60{x^2} + 23x - 1} \right)dx} \) ta có:
\(J = \left. {\left( {\frac{{50{x^4}}}{4} - \frac{{60{x^3}}}{3} + \frac{{23{x^2}}}{2} - x} \right)} \right|_0^1 = 3\)
Khi đó ta có \(\int\limits_0^1 {f\left( x \right)dx} + \frac{1}{2}\int\limits_0^1 {f\left( x \right)dx} = 3\)
\( \Leftrightarrow \frac{3}{2}\int\limits_0^1 {f\left( x \right)dx} = 3\)
\( \Leftrightarrow \int\limits_0^1 {f\left( x \right)dx} = 2\).
Câu 34:
Một bài trắc nghiệm có 10 câu hỏi, mỗi câu có 4 phương án lựa chọn trong đó chỉ có 1 phương án đúng. Mỗi câu đúng được 5 điểm, mỗi câu sai bị trừ 2 điểm. Một học sinh do không học bài nên đánh hú họa cho mỗi câu. Tính xác suất để học sinh đó nhận điểm dưới 1.
Đáp án A
Giải chi tiết:
Xác suất để trả lời đúng 1 câu là \(\frac{1}{4}\), xác suất để trả lời sai 1 câu là \[\frac{3}{4}\].
Gọi số câu trả lời đúng là \[x{\mkern 1mu} {\mkern 1mu} \left( {0 \le x \le 10,{\mkern 1mu} {\mkern 1mu} x \in \mathbb{N}} \right)\] thì số câu trả lời sai là \[10 - x\].
Số điểm học sinh đó đạt được là \[5x - 2\left( {10 - x} \right) = 7x - 20\].
Theo giả thiết \[ \Rightarrow 7x - 20 < 1 \Leftrightarrow 7x < 21 \Leftrightarrow x < 3 \Rightarrow x \in \left\{ {0;1;2} \right\}\].
TH1: Đúng 0 câu, sai 10 câu \[{P_1} = {\left( {\frac{3}{4}} \right)^{10}}\].
TH2: Đúng 1 câu, sai 9 câu \[{P_2} = C_{10}^1.\frac{1}{4}.{\left( {\frac{3}{4}} \right)^9}\].
TH3: Đúng 2 câu, sai 8 câu \[{P_3} = C_{10}^2.{\left( {\frac{1}{4}} \right)^2}.{\left( {\frac{3}{4}} \right)^8}\].
Vậy xác suất để học sinh đó nhận điểm dưới 1 là:
\[{\left( {\frac{3}{4}} \right)^{10}} + C_{10}^1.\frac{1}{4}.{\left( {\frac{3}{4}} \right)^9} + C_{10}^2.{\left( {\frac{1}{4}} \right)^2}.{\left( {\frac{3}{4}} \right)^8} \approx 0,53\].
Câu 35:
Cho tứ diện \[ABCD\] có \(AB,{\mkern 1mu} {\mkern 1mu} AC,{\mkern 1mu} {\mkern 1mu} AD\) đôi một vuông góc với \(AB = 6a\), \(AC = 9a\), \(AD = 3a\). Gọi \(M,{\mkern 1mu} {\mkern 1mu} N,{\mkern 1mu} {\mkern 1mu} P\) lần lượt là trọng tâm các tam giác \(ABC,{\mkern 1mu} {\mkern 1mu} ACD,{\mkern 1mu} {\mkern 1mu} ADB\). Thể tích của khối tứ diện \(AMNP\) bằng:
Đáp án A
Phương pháp giải:
- Gọi \({M_1},{\mkern 1mu} {\mkern 1mu} {N_1},{\mkern 1mu} {\mkern 1mu} {P_1}\) lần lượt là trung điểm của \(BC,{\mkern 1mu} {\mkern 1mu} CD,{\mkern 1mu} {\mkern 1mu} BD\), sử dụng công thức tỉ lệ thể tích Simpson, so sánh \({V_{AMNP}}\) và \({V_{A{M_1}{N_1}{P_1}}}\).
- Tiếp tục so sánh thể tích hai khối chóp có cùng chiều cao \(A.{M_1}{N_1}{P_1}\) và \(A.BCD\), sử dụng tam giác đồng dạng để suy ra tỉ số diện tích hai đáy.
- Tính thể tích khối tứ diện \(ABCD\)là \({V_{ABCD}} = \frac{1}{6}AB.AC.AD\), từ đó tính được \({V_{AMNP}}\).
Giải chi tiết:
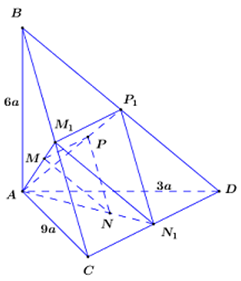
Gọi \({M_1},{\mkern 1mu} {\mkern 1mu} {N_1},{\mkern 1mu} {\mkern 1mu} {P_1}\) lần lượt là trung điểm của \(BC,{\mkern 1mu} {\mkern 1mu} CD,{\mkern 1mu} {\mkern 1mu} BD\), ta có:
\(\frac{{AM}}{{A{M_1}}} = \frac{{AN}}{{A{N_1}}} = \frac{{AP}}{{A{P_1}}} = \frac{2}{3}\)
Khi đó \(\frac{{{V_{AMNP}}}}{{{V_{A{M_1}{N_1}{P_1}}}}} = \frac{{AM}}{{A{M_1}}}.\frac{{AN}}{{A{N_1}}}.\frac{{AP}}{{A{P_1}}} = \frac{8}{{27}}\)
Dễ thấy \[\Delta {M_1}{N_1}{P_1}\] đồng dạng với tam giác \[DBC\] theo tỉ số \[k = \frac{1}{2}\] nên \[\frac{{{S_{{M_1}{N_1}{P_1}}}}}{{{S_{DBC}}}} = \frac{1}{4}\].
Mà hai khối chóp \[A.{M_1}{N_1}{P_1}\] và \[A.BCD\] có cùng chiều cao nên \(\frac{{{V_{A.{M_1}{N_1}{P_1}}}}}{{{V_{ABCD}}}} = \frac{{{S_{{M_1}{N_1}{P_1}}}}}{{{S_{DBC}}}} = \frac{1}{4}\).
Lại có \({V_{ABCD}} = \frac{1}{6}AB.AC.AD = \frac{1}{6}.6a.9a.3a = 27{a^3}\).
\( \Rightarrow {V_{A.{M_1}{N_1}{P_1}}} = \frac{1}{4}{V_{ABCD}} = \frac{{27{a^3}}}{4}\)
Vậy \({V_{AMNP}} = \frac{8}{{27}}{V_{A{M_1}{N_1}{P_1}}} = \frac{8}{{27}}.\frac{{27{a^3}}}{4} = 2{a^3}\).
Câu 36:
Tiếp tuyến của đồ thị hàm số \(y = \frac{{x + 1}}{{2x - 3}}\) tại điểm có hoành độ \({x_0} = - 1\) có hệ số góc bằng bao nhiêu?
Đáp án: \( - \frac{1}{5}\)
Phương pháp giải:
Hệ số góc của đồ thị hàm số \(y = f\left( x \right)\) tại điểm có hoành độ \(x = {x_0}\) là \(k = f'\left( {{x_0}} \right)\).
Giải chi tiết:
TXĐ: \(D = \mathbb{R}\backslash \left\{ {\frac{3}{2}} \right\}\).
Ta có: \(y' = \frac{{ - 5}}{{{{\left( {2x - 3} \right)}^2}}}\).
Vậy hệ số góc của tiếp tuyến của đồ thị hàm số \(y = \frac{{x + 1}}{{2x - 3}}\) tại điểm có hoành độ \({x_0} = - 1\) là:
\(k = y'\left( { - 1} \right) = \frac{{ - 5}}{{{{\left( { - 5} \right)}^2}}} = - \frac{1}{5}\).
Câu 37:
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = \left( {\ln x + 1} \right)\left( {{e^x} - 2019} \right)\left( {x + 1} \right)\) trên khoảng \(\left( {0; + \infty } \right)\). Hỏi hàm số \(y = f\left( x \right)\) có bao nhiêu điểm cực trị?
Đáp án: 2
Phương pháp giải:
Giải phương trình \(f'\left( x \right) = 0\) xác định số điểm cực trị bằng số nghiệm bội lẻ của phương trình \(f'\left( x \right) = 0\).
Giải chi tiết:
TXĐ: \(D = \left( {0; + \infty } \right)\).
Ta có: \(f'\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\ln x + 1 = 0}\\{{e^x} - 2019 = 0}\\{x + 1 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\ln x = - 1}\\{{e^x} = 2019}\\{x = - 1}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{1}{e} \in \left( {0; + \infty } \right)}\\{x = \ln 2019 \in \left( {0; + \infty } \right)}\\{x = - 1 \notin \left( {0; + \infty } \right)}\end{array}} \right.\)
Vậy hàm số đã cho có 2 điểm cực trị.
Câu 38:
Trong không gian Oxyz, tính khoảng cách giữa hai mặt phẳng \(\left( P \right):{\mkern 1mu} {\mkern 1mu} 2x + 2y - z - 11 = 0\)và \(\left( Q \right):{\mkern 1mu} {\mkern 1mu} 2x + 2y - z + 4 = 0\).
Đáp án: \(d\left( {\left( P \right),\left( Q \right)} \right) = 5\)
Phương pháp giải:
Tính khoảng cách giữa 2 mặt phẳng song song \(Ax + By + Cz + D = 0\) và \(Ax + By + Cz + D' = 0\) là \(d = \frac{{\left| {D - D'} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\).
Giải chi tiết:
\(d\left( {\left( P \right),\left( Q \right)} \right) = \frac{{\left| { - 11 - 4} \right|}}{{\sqrt {{2^2} + {2^2} + {{\left( { - 1} \right)}^2}} }} = 5.\)
Câu 39:
Trong kì thi học sinh giỏi có 10 học sinh đạt tối đa điểm môn Toán trong đó có 4 học sinh nam và 6 học sinh nữ. Nhà trường muốn chọn một nhóm 5 học sinh trong 10 học sinh trên để tham dự buổi lễ tuyên dương khen thưởng. Tính số cách chọn một nhóm gồm 5 học sinh mà có cả nam và nữ và số học sinh nam ít hơn số học sinh nữ.
Đáp án: 180
Phương pháp giải:
Xét các TH:
TH1: 1 nam + 4 nữ.
TH2: 2 nam + 3 nữ.
Giải chi tiết:
TH1: Chọn 1 học sinh nam và 4 học sinh nữ có \(C_4^1.C_6^4 = 60\) cách.
TH2: Chọn 2 học sinh nam và 3 học sinh nữ có \(C_4^2.C_6^3 = 120\) cách.
Vậy có tất cả \(60 + 120 = 180\) cách chọn 5 học sinh mà có cả nam và nữ, đồng thời số học sinh nam ít hơn số học sinh nữ.
Câu 40:
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và \(\mathop {\lim }\limits_{x \to 2} \frac{{f\left( x \right) - 1}}{{{x^2} - x - 2}} = 3\). Tính \(\mathop {\lim }\limits_{x \to 2} \frac{{{f^3}\left( x \right) + 3f\left( x \right) - 4}}{{{x^2} - 2x}}\).
Đáp án: 27
Phương pháp giải:
- Đặt \(\frac{{f\left( x \right) - 1}}{{{x^2} - x - 2}} = g\left( x \right)\), biểu diễn \(f\left( x \right)\) theo \(g\left( x \right)\) và tìm \(\mathop {\lim }\limits_{x \to 2} f\left( x \right)\).
- Phân tích biểu thức \(\frac{{{f^3}\left( x \right) + 3f\left( x \right) - 4}}{{{x^2} - 2x}}\) thành tích 2 phân thức, 1 phân thức dạng \(\frac{0}{0}\) và một phân thức xác định.
- Dựa vào giới hạn đề bài.
Giải chi tiết:
Đặt \(\frac{{f\left( x \right) - 1}}{{{x^2} - x - 2}} = g\left( x \right) \Rightarrow f\left( x \right) = \left( {{x^2} - x - 2} \right)g\left( x \right) + 1\)
Khi đó ta có: \(\mathop {\lim }\limits_{x \to 2} \frac{{f\left( x \right) - 1}}{{{x^2} - x - 2}} = 3 \Rightarrow \mathop {\lim }\limits_{x \to 2} g\left( x \right) = 3\)
\( \Rightarrow \mathop {\lim }\limits_{x \to 2} f\left( x \right) = \mathop {\lim }\limits_{x \to 2} \left[ {\left( {{x^2} - x - 2} \right)g\left( x \right) + 1} \right] = 1\)
Ta có: \({\mkern 1mu} \mathop {\lim }\limits_{x \to 2} \frac{{{f^3}\left( x \right) + 3f\left( x \right) - 4}}{{{x^2} - 2x}}\)
\( = \mathop {\lim }\limits_{x \to 2} \frac{{\left[ {f\left( x \right) - 1} \right]\left[ {{f^2}\left( x \right) + f\left( x \right) + 4} \right]}}{{x\left( {x - 2} \right)}}\)
\( = \mathop {\lim }\limits_{x \to 2} \frac{{f\left( x \right) - 1}}{{x - 2}}.\mathop {\lim }\limits_{x \to 2} \frac{{{f^2}\left( x \right) + f\left( x \right) + 4}}{x}\)
Theo bài ra ta có: \(\mathop {\lim }\limits_{x \to 2} \frac{{f\left( x \right) - 1}}{{{x^2} - x - 2}} = 3\)
\( \Rightarrow \mathop {\lim }\limits_{x \to 2} \frac{{f\left( x \right) - 1}}{{\left( {x - 2} \right)\left( {x + 1} \right)}} = 3\)
\( \Leftrightarrow \mathop {\lim }\limits_{x \to 2} \frac{{f\left( x \right) - 1}}{{x - 2}}.\frac{1}{{x + 1}} = 3\)
\( \Leftrightarrow \mathop {\lim }\limits_{x \to 2} \frac{{f\left( x \right) - 1}}{{x - 2}}.\mathop {\lim }\limits_{x \to 2} \frac{1}{{x + 1}} = 3\)
\( \Leftrightarrow \mathop {\lim }\limits_{x \to 2} \frac{{f\left( x \right) - 1}}{{x - 2}}.\frac{1}{3} = 3\)
\( \Leftrightarrow \mathop {\lim }\limits_{x \to 2} \frac{{f\left( x \right) - 1}}{{x - 2}} = 9\)
Vậy \(\mathop {\lim }\limits_{x \to 2} \frac{{{f^3}\left( x \right) + 3f\left( x \right) - 4}}{{{x^2} - 2x}} = 9.\frac{{1 + 1 + 4}}{2} = 27\).
Câu 41:
Giá trị nhỏ nhất của hàm số \(y = {x^2} - 4x + 5\) là?
Đáp án: 1
Phương pháp giải:
Cho hàm số \(y = a{x^2} + bx + c\left( {a \ne 0} \right)\)
Với \(a > 0:\) Giá trị nhỏ nhất của hàm số \({y_{\min }} = - \frac{\Delta }{{4a}}\) đạt được tại \(x = - \frac{b}{{2a}}.\)
Với \(a < 0:\) Giá trị lớn nhất của hàm số \({y_{\max }} = - \frac{\Delta }{{4a}}\) ạt được tại \(x = - \frac{b}{{2a}}.\)
Giải chi tiết:
Hoành độ đỉnh \(x = - \frac{b}{{2a}} = - \frac{{ - 4}}{2} = 2.\)
Vì \(a = 1 > 0\) nên hàm số \(y = {x^2} - 4x + 5\) có giá trị nhỏ nhất \({y_{\min }} = y\left( 2 \right) = {2^2} - 4.2 + 5 = 1.\)
Câu 42:
Tìm tham số \(m\) để hàm số \(y = \frac{1}{3}{x^3} - m{x^2} + \left( {m + 2} \right)x + 2018\) không có cực trị?
Đáp án: \[ - 1 \le m \le 2\]
Phương pháp giải:
- Tính đạo hàm.
- Hàm số không có cực trị \[ \Leftrightarrow y' = 0\] vô nghiệm hoặc có nghiệm kép \[ \Leftrightarrow \Delta \le 0\].
Giải chi tiết:
+ \(y' = {x^2} - 2mx + m + 2{\mkern 1mu} {\mkern 1mu} \left( 1 \right)\)
+ Hàm số không có cực trị \( \Leftrightarrow \left( 1 \right)\) vô nghiệm hoặc có nghiệm kép \( \Leftrightarrow \Delta \le 0\)
\( \Leftrightarrow {\left( { - 2m} \right)^2} - 4.1.\left( {m + 2} \right) \le 0\)
\( \Leftrightarrow 4{m^2} - 4m - 8 \le 0\)
\( \Leftrightarrow - 1 \le m \le 2\).
Câu 43:
Tính diện tích \(S\) của hình phẳng \(\left( H \right)\) giới hạn bởi các đường cong \(y = - {x^3} + 12x\) và \(y = - {x^2}\).
Đáp án: \(S = \frac{{937}}{{12}}\)
Phương pháp giải:
- Giải phương trình hoành độ giao điểm.
- Sử dụng công thức: Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right),{\mkern 1mu} {\mkern 1mu} y = g\left( x \right)\), các đường thẳng \(x = a,{\mkern 1mu} {\mkern 1mu} x = b\) là \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).
Giải chi tiết:
Xét phương trình hoành độ giao điểm:
\( - {x^3} + 12x = - {x^2} \Leftrightarrow - {x^3} + {x^2} + 12x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 4}\\{x = - 3}\end{array}} \right.\)
Vậy diện tích của hình phẳng \(\left( H \right)\) là:
\(\int\limits_{ - 3}^0 {\left| { - {x^3} + {x^2} + 12x} \right|} + \int\limits_0^4 {\left| { - {x^3} + {x^2} + 12x} \right|} = \frac{{99}}{4} + \frac{{160}}{3} = \frac{{937}}{{12}}\).
Câu 44:
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ.
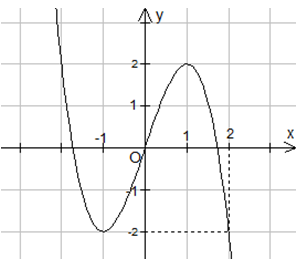
Số nghiệm của phương trình \(f\left( {f\left( x \right)} \right) = - 2\) là
Đáp án: 5
Phương pháp giải:
- Đặt \(t = f\left( x \right)\), dựa vào tương giao đồ thị giải phương trình tìm t.
- Tiếp tục sử dụng tương giao tìm số nghiệm x.
Giải chi tiết:
Đặt \(t = f\left( x \right)\), phương trình trở thành \(f\left( t \right) = - 2\).
Số nghiệm của phương trình bằng số giao điểm của đồ thị hàm số \(y = f\left( t \right)\) và đường thẳng \(y = - 2\).
Dựa vào đồ thị hàm số ta thấy: Phương trình có nghiệm \(\left[ {\begin{array}{*{20}{l}}{t = - 2}\\{t = 1}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{f\left( x \right) = - 2}\\{f\left( x \right) = 1}\end{array}} \right.\).
Tiếp tục dựa vào đồ thị hàm số ta thấy:
Phương trình \(f\left( x \right) = - 2\) có 2 nghiệm phân biệt.
Phương trình \(f\left( x \right) = 1\) có 3 nghiệm phân biệt.
Vậy phương trình ban đầu có tất cả 5 nghiệm phân biệt.
Câu 45:
Tính giá trị biểu thức \(T = {\left| {{z_1} - {z_2}} \right|^2}\), biết \({z_1},{z_2}\) là các số phức thỏa mãn đồng thời \(\left| z \right| = 5\) và \(\left| {z - \left( {7 + 7i} \right)} \right| = 5\).
Đáp án: 2
Phương pháp giải:
- Đặt \(z = a + bi\), thay vào các điều kiện bài cho lập hệ phương trình ẩn \(x,y\).
- Giải hệ phương trình tìm \(x,y \Rightarrow z\).
Giải chi tiết:
Đặt \(z = a + bi\) ta có:
\(\left\{ {\begin{array}{*{20}{l}}{\left| z \right| = 5}\\{\left| {z - \left( {7 + 7i} \right)} \right| = 5}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{a^2} + {b^2} = 25}\\{{{\left( {a - 7} \right)}^2} + {{\left( {b - 7} \right)}^2} = 25}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{a^2} + {b^2} = 25}\\{{a^2} + {b^2} - 14a - 14b + 98 = 25}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{a^2} + {b^2} = 25}\\{a + b = 7}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{b = 7 - a}\\{{a^2} + {{\left( {7 - a} \right)}^2} = 25}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{b = 7 - a}\\{2{a^2} - 14a + 24 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{a = 4,b = 3}\\{a = 3,b = 4}\end{array}} \right.\)
\( \Rightarrow \) hai số phức cần tìm là \(4 + 3i,3 + 4i \Rightarrow T = {\left| {{z_1} - {z_2}} \right|^2} = {\left| {\left( {4 + 3i} \right) - \left( {3 + 4i} \right)} \right|^2} = {\left| {1 - i} \right|^2} = 2\).
Câu 46:
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AA' = a,\) \(AD = a\sqrt 3 \). Góc giữa hai mặt phẳng \(\left( {ABC'D'} \right)\) và \(\left( {ABCD} \right)\) bằng:
Đáp án: \[30^\circ \]
Phương pháp giải:
- Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.
- Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông để tính góc.
Giải chi tiết:
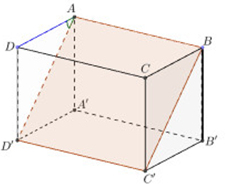
Ta có: \[AB \bot \left( {ADD'A'} \right) \Rightarrow AB \bot AD'\]
\(\left\{ {\begin{array}{*{20}{l}}{\left( {ABC'D'} \right) \cap \left( {ABCD} \right) = AB}\\{AD \subset \left( {ABCD} \right);{\mkern 1mu} {\mkern 1mu} AD \bot AB}\\{AD' \subset \left( {ABC'D'} \right);{\mkern 1mu} {\mkern 1mu} AD' \bot AB}\end{array}} \right.\)
\( \Rightarrow \angle \left( {\left( {ABC'D'} \right);\left( {ABCD} \right)} \right) = \angle \left( {AD;AD'} \right) = \angle DAD'\)
Xét tam giác vuông \(ADD'\) có: \(\tan \angle DAD' = \frac{{DD'}}{{AD}} = \frac{a}{{a\sqrt 3 }} = \frac{1}{{\sqrt 3 }}\)
\( \Rightarrow \angle DAD' = {30^0}\)
Vậy \(\angle \left( {\left( {ABC'D'} \right);\left( {ABCD} \right)} \right) = {30^0}\).
Câu 47:
Trong không gian với hệ tọa độ \(Oxyz\), cho mặt phẳng \(\left( P \right):{\mkern 1mu} {\mkern 1mu} 2x - 2y - z + 7 = 0\) và điểm \(A\left( {1;1; - 2} \right)\). Điểm \(H\left( {a;b;c} \right)\) là hình chiếu vuông góc của \(A\) trên \(\left( P \right)\). Tổng \(a + b + c\) bằng:
Đáp án: 1
Phương pháp giải:
- Viết phương trình đường thẳng Δ đi qua A và vuông góc với \(\left( P \right)\).
- Tìm \(H = \Delta \cap \left( P \right)\).
- Tìm \(a,{\mkern 1mu} {\mkern 1mu} b,{\mkern 1mu} {\mkern 1mu} c\) và tính tổng.
Giải chi tiết:
Gọi Δ là đường thẳng đi qua \(A\) và vuông góc với \(\left( P \right)\), phương trình đường thẳng Δ là:
\(\left\{ {\begin{array}{*{20}{l}}{x = 1 + 2t}\\{y = 1 - 2t}\\{z = - 2 - t}\end{array}} \right.{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( \Delta \right)\)
Vì \(H\) là hình chiếu vuông góc của A trên \(\left( P \right)\) nên \[H = \Delta \cap \left( P \right)\]
\[ \Rightarrow \] Tọa độ điểm \[H\] là nghiệm của hệ phương trình:
\[\left\{ {\begin{array}{*{20}{l}}{x = 1 + 2t}\\{y = 1 - 2t}\\{z = - 2 - t}\\{2x - 2y - z + 7 = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 1 + 2t}\\{y = 1 - 2t}\\{z = - 2 - t}\\{2 + 4t - 2 + 4t + 2 + t + 7 = 0}\end{array}} \right.\]
\[ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 1 + 2t}\\{y = 1 - 2t}\\{z = - 2 - t}\\{9t + 9 = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{t = - 1}\\{x = - 1}\\{y = 3}\\{z = - 1}\end{array}} \right. \Rightarrow H\left( { - 1;3; - 1} \right)\]
\[ \Rightarrow a = - 1,{\mkern 1mu} {\mkern 1mu} b = 3,{\mkern 1mu} {\mkern 1mu} c = - 1\]
Vậy \[a + b + c = - 1 + 3 - 1 = 1\].
Câu 48:
Xét các số thực dương a và b thỏa mãn \[{\log _3}\left( {1 + ab} \right) = \frac{1}{2} + {\log _3}\left( {b - a} \right)\]. Giá trị nhỏ nhất của biểu thức \(P = \frac{{\left( {1 + {a^2}} \right)\left( {1 + {b^2}} \right)}}{{a\left( {a + b} \right)}}\)bằng:
Đáp án: 4
Giải chi tiết:
ĐKXĐ: \(\left\{ {\begin{array}{*{20}{l}}{b - a > 0}\\{a,{\mkern 1mu} {\mkern 1mu} b > 0}\end{array}} \right.\).
Ta có: \({\log _3}\left( {1 + ab} \right) = \frac{1}{2} + {\log _3}\left( {b - a} \right)\)
\( \Leftrightarrow {\log _3}\left( {1 + ab} \right) - {\log _3}\left( {b - a} \right) = \frac{1}{2}\)
\( \Leftrightarrow {\log _3}\frac{{1 + ab}}{{b - a}} = \frac{1}{2}\)
\( \Leftrightarrow \frac{{1 + ab}}{{b - a}} = \sqrt 3 \)
\( \Leftrightarrow 1 + ab = \sqrt 3 \left( {b - a} \right)\)
\( \Leftrightarrow \frac{1}{a} + b = \sqrt 3 \left( {\frac{b}{a} - 1} \right)\).
Áp dụng BĐT Cô-si ta có \(\frac{1}{a} + b \ge 2\sqrt {\frac{b}{a}} \) nên
\(\sqrt 3 \left( {\frac{b}{a} - 1} \right) \ge 2\sqrt {\frac{b}{a}} \Leftrightarrow \sqrt 3 \frac{b}{a} - 2\sqrt {\frac{b}{a}} - \sqrt 3 \ge 0\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\sqrt {\frac{b}{a}} \ge \sqrt 3 }\\{\sqrt {\frac{b}{a}} \le - \frac{1}{{\sqrt 3 }}{\mkern 1mu} {\mkern 1mu} \left( {Loai} \right)}\end{array}} \right. \Leftrightarrow \sqrt {\frac{b}{a}} \ge \sqrt 3 \Leftrightarrow \frac{b}{a} \ge 3\)
Ta có: \(P = \frac{{\left( {1 + {a^2}} \right)\left( {1 + {b^2}} \right)}}{{a\left( {a + b} \right)}} = \frac{{1 + {a^2} + {b^2} + {a^2}{b^2}}}{{a\left( {a + b} \right)}}\)
Áp dụng BĐT Cô-si ta có \(1 + {a^2}{b^2} \ge 2\sqrt {{a^2}{b^2}} = 2ab\) nên
\(1 + {a^2} + {b^2} + {a^2}{b^2} \ge {a^2} + {b^2} + 2ab = {\left( {a + b} \right)^2}\)
\( \Rightarrow P = \frac{{1 + {a^2} + {b^2} + {a^2}{b^2}}}{{a\left( {a + b} \right)}} \ge \frac{{{{\left( {a + b} \right)}^2}}}{{a\left( {a + b} \right)}} = \frac{{a + b}}{a} = 1 + \frac{b}{a} \ge 4\)
Vậy \({P_{\min }} = 4 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\frac{1}{a} = b}\\{\frac{b}{a} = 3}\\{a,{\mkern 1mu} {\mkern 1mu} b > 0,{\mkern 1mu} {\mkern 1mu} b - a > 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\frac{1}{a} = 3a}\\{b = 3a}\\{a,{\mkern 1mu} {\mkern 1mu} b > 0,{\mkern 1mu} {\mkern 1mu} b - a > 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = \frac{1}{{\sqrt 3 }}}\\{b = \sqrt 3 }\end{array}} \right.\).
Câu 49:
Cho tứ diện \(OABC\) có ba cạnh \(OA,{\mkern 1mu} {\mkern 1mu} OB,{\mkern 1mu} {\mkern 1mu} OC\) đôi một vuông góc với nhau. Biết khoảng cách từ điểm \(O\) đến các đường thẳng \(BC,{\mkern 1mu} {\mkern 1mu} CA,{\mkern 1mu} {\mkern 1mu} AB\) lần lượt là \(a,{\mkern 1mu} {\mkern 1mu} a\sqrt 2 ,{\mkern 1mu} {\mkern 1mu} a\sqrt 3 \). Tính khoảng cách từ điểm \(O\) đến mặt phẳng \(\left( {ABC} \right)\) theo a.
Đáp án: \(\frac{{2a\sqrt {33} }}{{11}}\)
Phương pháp giải:
- Kẻ \(OM \bot AC{\mkern 1mu} {\mkern 1mu} \left( {M \in AC} \right)\), \(ON \bot AB{\mkern 1mu} {\mkern 1mu} \left( {N \in AB} \right)\), \(OP \bot BC{\mkern 1mu} {\mkern 1mu} \left( {P \in BC} \right)\). Khi đó ta có \(OP = a,\) \(OM = a\sqrt 2 ,\) \(ON = a\sqrt 3 \).
- Trong \[\left( {OCN} \right)\] kẻ \[OH \bot CN{\mkern 1mu} {\mkern 1mu} \left( {H \in CN} \right)\], chứng minh \[OH \bot \left( {ABC} \right)\].
- Sử dụng hệ thức lượng trong tam giác vuông để tính khoảng cách.
Giải chi tiết:
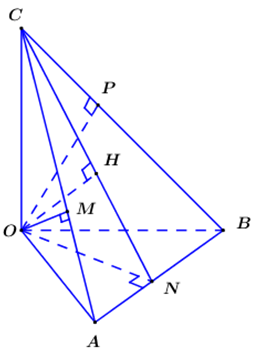
Kẻ \(OM \bot AC{\mkern 1mu} {\mkern 1mu} \left( {M \in AC} \right)\), \(ON \bot AB{\mkern 1mu} {\mkern 1mu} \left( {N \in AB} \right)\), \(OP \bot BC{\mkern 1mu} {\mkern 1mu} \left( {P \in BC} \right)\)
Khi đó ta có \[OP = a,{\mkern 1mu} {\mkern 1mu} OM = a\sqrt 2 ,{\mkern 1mu} {\mkern 1mu} ON = a\sqrt 3 \]
Trong \(\left( {OCN} \right)\) kẻ \(OH \bot CN{\mkern 1mu} {\mkern 1mu} \left( {H \in CN} \right)\) ta có:
\(\left\{ {\begin{array}{*{20}{l}}{AB \bot ON}\\{AB \bot OC}\end{array}} \right. \Rightarrow AB \bot \left( {OCN} \right) \Rightarrow AB \bot OH\)
\(\left\{ {\begin{array}{*{20}{l}}{OH \bot AB}\\{OH \bot CN}\end{array}} \right. \Rightarrow OH \bot \left( {ABC} \right) \Rightarrow d\left( {O;\left( {ABC} \right)} \right) = OH\)
Áp dụng hệ thức lượng trong tam giác vuông ta có:
\(\frac{1}{{O{H^2}}} = \frac{1}{{O{C^2}}} + \frac{1}{{O{N^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\)
Lại có: \(\frac{1}{{O{M^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{C^2}}};{\mkern 1mu} {\mkern 1mu} \frac{1}{{O{N^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}};{\mkern 1mu} {\mkern 1mu} \frac{1}{{O{P^2}}} = \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\)
\( \Rightarrow \frac{1}{{O{M^2}}} + \frac{1}{{O{N^2}}} + \frac{1}{{O{P^2}}} = 2\left( {\frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}} \right)\)
\( \Rightarrow \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}} = \frac{1}{2}\left( {\frac{1}{{O{M^2}}} + \frac{1}{{O{N^2}}} + \frac{1}{{O{P^2}}}} \right)\)
\( \Rightarrow \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}} = \frac{1}{2}\left( {\frac{1}{{2{a^2}}} + \frac{1}{{3{a^2}}} + \frac{1}{{{a^2}}}} \right) = \frac{{11}}{{12{a^2}}}\)
\( \Rightarrow \frac{1}{{O{H^2}}} = \frac{{11}}{{12{a^2}}} \Rightarrow OH = \frac{{2a\sqrt {33} }}{{11}}\)
Vậy \(d\left( {O;\left( {ABC} \right)} \right) = \frac{{2a\sqrt {33} }}{{11}}\).
Câu 50:
Ông A dự định sử dụng hết \(6,5{m^3}\) kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
Đáp án: \(1,50{\mkern 1mu} {m^3}\)
Phương pháp giải:
- Gọi chiều rộng, chiều dài, chiều cao của bể lần lượt là \(x,2x,y\)
- Tìm mối liên hệ \(x,y\) dựa vào dữ kiện diện tích \(6,5{m^2}\).
- Lập hàm số thể tích theo ẩn \(x\) và xét hàm tìm \({V_{\max }}\).
Giải chi tiết: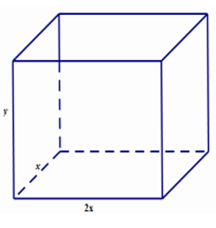
Gọi chiều rộng, chiều dài, chiều cao của bể lần lượt là \(x,2x,y{\mkern 1mu} {\mkern 1mu} \left( {x,y > 0} \right)\).
Diện tích phần lắp kính là: \(2x.x + 2xy + 2.2x.y = 2{x^2} + 6xy = 6,5\)
\( \Leftrightarrow xy = \frac{{6,5 - 2{x^2}}}{6} > 0 \Rightarrow x < \sqrt {\frac{{6,5}}{2}} = \frac{{\sqrt {13} }}{2}.\)
Thể tích bể cá là: \(V = 2x.x.y = 2x.\frac{{6,5 - 2{x^2}}}{6} = \frac{{ - 4{x^3} + 13x}}{6}\) với \(0 < x < \frac{{\sqrt {13} }}{2}\)
Ta có: \(V' = \frac{{ - 12{x^2} + 13}}{6},V' = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{{\sqrt {39} }}{6}}\\{x = - \frac{{\sqrt {39} }}{6}\left( L \right)}\end{array}} \right.\)
Bảng biến thiên:
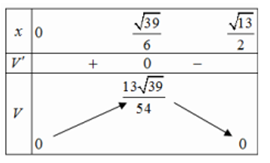
Vậy \({V_{\max }} = \frac{{13\sqrt {39} }}{{54}} \approx 1,50{\mkern 1mu} {m^3}\).
Câu 51:
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 51 đến 55:
Tây Tiến đoàn binh không mọc tóc
Quân xanh màu lá dữ oai hùm
Mắt trừng gửi mộng qua biên giới
Đêm mơ Hà Nội dáng Kiều thơm
Rải rác biên cương mồ viễn xứ
Chiến trường đi chẳng tiếc đời xanh
Áo bào thay chiếu anh về đất
Sông Mã gầm lên khúc độc hành
(Trích Tây Tiến, Quang Dũng, SGK Ngữ văn lớp 12, tập 1, trang 83)
Đoạn thơ trên được trích từ tập thơ nào?
Đáp án D
Phương pháp giải:
Căn cứ xuất xứ bài thơ Tây Tiến
Giải chi tiết:
Tác phẩm Tây Tiến được trích trong tập “Mây đầu ô” sáng tác năm 1948 khi Quang Dũng phải chuyển công tác đên làng Phù Lưu Chanh. Tại đây, ông nhớ đồng đội và làm bài thơ này.
Câu 52:
Cụm từ “quân xanh màu lá” trong câu “quân xanh màu lá dữ oai hùm” nhằm chỉ điều gì?
Đáp án A
Phương pháp giải:
Căn cứ nội dung bài Tây Tiến.
Giải chi tiết:
Cụm từ: “Quân xanh màu lá dữ oai hùm” là để chỉ hình ảnh những người lính bị sốt rét khiến nước da của họ tái mét đi như màu xanh của lá cây. Cách nói này không những không bi lụy mà
Câu 53:
Hình ảnh con sông Mã được xuất hiện trong đoạn thơ trên có mối liên hệ như thế nào với hình ảnh con sông Mã xuất hiện ở khổ thơ đầu?
Đáp án A
Phương pháp giải:
Căn cứ vào nghệ thuật bài thơ Tây Tiến
Giải chi tiết:
Hình ảnh con sông Mã được xuất hiện trong đoạn thơ trên kết hợp với hình ảnh sông Mã ở khổ thơ đầu tạo nên kết cấu đầu cuối tương ứng.
Câu 54:
Câu thơ nào nói đến vẻ đẹp hào hoa của người lính Tây Tiến?
Đáp án B
Phương pháp giải:
Căn cứ vào nội dung của tác phẩm Tây Tiến
Giải chi tiết:
Hai câu: “Mắt trừng gửi mộng qua biên giới/ Đêm mơ Hà Nội dáng Kiều thơm” nói đến vẻ đẹp hào hoa của người lính Tây Tiến. Trong hoàn cảnh chiến tranh ác liệt người lính tây Tiến vẫn nhớ tới một “dáng kiều thơm”. Ở đây có thể hiểu cụm từ nhằm để chỉ những người con gái xinh đẹp, đáng yêu. Một thời gian câu thơ này bị cho là rơi rớt chất tiểu tư sản nhưng về sau tác phẩm đã lấy lại vị thế và câu thơ được hiểu theo hướng tích cực. Nhớ về dáng người con gái (người yêu) giữa nơi bom rơi đạn lạc cho thấy chất hào hoa của những người lính trẻ đồng thời chính là động lực để người lính tiếp tục cuộc chiến ác liệt bảo vệ quê hương.
Câu 55:
Phong cách ngôn ngữ nào được sử dụng trong văn bản trên?
Đáp án C
Phương pháp giải:
Căn cứ vào các loại phong cách ngôn ngữ đã học
Giải chi tiết:
Phong cách ngôn ngữ nghệ thuật thường xuất hiện trong các tác phẩm nghệ thuật. Nó là ngôn ngữ được tổ chức, sắp xếp, lựa chọn, gọt giũa, tinh luyện từ ngôn ngữ thông thường và đạt được giá trị nghệ thuật – thẩm mĩ.
-> Đoạn trích trên thuộc phong cách ngôn ngữ: Nghệ thuật
Câu 56:
Dựa vào các thông tin được cung cấp dưới đây để trả lời các câu từ 56 đến 60:
“Bạn cũ ngồi than thở, nói ghét Sài Gòn lắm, chán Sài Gòn lắm, trời ơi, thèm ngồi giữa rơm rạ quê nhà lắm, nhớ Bé Năm Bé Chín lắm. Lần nào gặp nhau thì cũng nói nội dung đó, có lúc người nghe bực quá bèn hỏi vặt vẹo, nhớ sao không về. Bạn tròn mắt, về sao được, con cái học hành ở đây, công việc ở đây, miếng ăn ở đây.
Nghĩ, thương thành phố, thấy thành phố sao giống cô vợ dại dột, sống với anh chồng thẳng thừng tôi
không yêu cô, nhưng rồi đến bữa cơm, anh ta lại về nhà với vẻ mặt quạu đeo, đói meo, vợ vẫn mỉm cười dọn lên những món ăn ngon nhất mà cô có. Vừa ăn chồng vừa nói tôi không yêu cô. Ăn no anh chồng vẫn nói tôi không yêu cô. Cô nàng mù quáng chỉ thản nhiên mỉm cười, lo toan nấu nướng cho bữa chiều, bữa tối.
Bằng cách đó, thành phố yêu anh. Phố cũng không cần anh đáp lại tình yêu, không cần tìm cách xóa sạch đi quá khứ, bởi cũng chẳng cách nào người ta quên bỏ được thời thơ ấu, mối tình đầu. Của rạ của rơm, của khói đốt đồng, vườn cau, rặng bần... bên mé rạch. Lũ cá rúc vào những cái vũng nước quánh đi dưới nắng. Bầy chim trao trảo lao xao kêu quanh quầy chuối chín cây. Ai đó cất tiếng gọi trẻ con về bữa cơm chiều, chén đũa khua trong cái mùi thơm quặn của nồi kho quẹt. Xao động đến từng chi tiết nhỏ”.
(Trích Yêu người ngóng núi, Nguyễn Ngọc Tư)
Đáp án A
Phương pháp giải:
Căn cứ đặc điểm các phong cách ngôn ngữ đã học
Giải chi tiết:
- Phong cách ngôn ngữ nghệ thuật là ngôn ngữ chủ yếu dùng trong các tác phẩm văn chương, không chỉ có chức năng thông tin mà còn thỏa mãn nhu cầu thẩm mĩ của con người. Nó là ngôn ngữ được tổ chức, xếp đặt, lựa chọn, tinh luyện từ ngôn ngữ thông thường và đạt được giá trị nghệ thuật – thẩm mĩ.
- Đặc trưng cơ bản:
+ Tính hình tượng
+ Tính truyền cảm
+ Tính cá thể hóa
- Đoạn văn trên thỏa mãn các đặc trưng cơ bản của ngôn ngữ nghệ thuật.
+ Tính hình tượng: Hình tượng “thành phố” được xây dựng bằng những biện pháp nghệ thuật so sánh (như cô vợ dại dột) và nhân hóa (phố cũng yêu anh). Từ đó tác giả khái quát thành sự cưu mang của thành phố đối với con người và tình cảm con người dành cho thành phố.
+ Tính truyền cảm: Bằng việc sử dụng những thủ pháp nghệ thuật so sánh và nhân hóa, tác giả đã khơi gợi được lòng đồng cảm của người đọc với những tâm tư của nhân vật trong đoạn văn: sự buồn chán thành phố nhưng vì những nhu cầu mưu sinh mà vẫn phải gắn bó, sự tiếc nuối kí ức tuổi thơ.
+ Tính cá thể hóa: Đoạn văn mang đậm phong cách của nhà văn Nguyễn Ngọc Tư: tình cảm, day dứt và nhiều suy tư
Câu 57:
Đáp án C
Phương pháp giải:
Căn cứ vào bài Từ ngữ địa phương và biệt ngữ xã hội
Giải chi tiết:
Từ “quạu đeo” là phương ngữ miền Nam, chỉ trạng thái con người nhăn nhó vì bực dọc, khó chịu.
Câu 58:
Phương thức biểu đạt chủ yếu của những câu văn: “Lũ cá rúc vào những cái vũng nước quánh đi dưới nắng. Bầy chim trao trảo lao xao kêu quanh quầy chuối chín cây…” là:
Đáp án A
Phương pháp giải:
Căn cứ vào đặc điểm của các phương thức biểu đạt đã học
Giải chi tiết:
Miêu tả là sử dụng ngôn ngữ hoặc màu sắc, đường nét, nhạc điệu để làm cho người khác hình dung được hình thức các sự vật hoặc hình dáng, tâm trạng trong khung cảnh nào đó.
Câu 59:
Trong đoạn văn thứ 3, “mối tình đầu” của “anh” là:
Đáp án A
Phương pháp giải:
Đọc, tìm ý
Giải chi tiết:
Căn cứ vào các câu văn: Phố cũng không cần anh đáp lại tình yêu, không cần tìm cách xóa sạch đi quá khứ, bởi cũng chẳng cách nào người ta quên bỏ được thời thơ ấu, mối tình đầu. Của rạ của rơm, của khói đốt đồng, vườn cau, rặng bần... bên mé rạch. Lũ cá rúc vào những cái vũng nước quánh đi dưới nắng. Bầy chim trao trảo lao xao kêu quanh quầy chuối chín cây. Ai đó cất tiếng gọi trẻ con về bữa cơm chiều, chén đũa khua trong cái mùi thơm quặn của nồi kho quẹt.
Câu 60:
Chủ đề chính của đoạn văn là:
Đáp án B
Phương pháp giải:
Căn cứ nội dung đoạn văn
Giải chi tiết:
Đoạn văn viết về sự nuôi sống, đùm bọc của mảnh đất Sài Gòn dành cho nhân vật trữ tình.
Câu 61:
Đọc đoạn trích sau và thực hiện các câu hỏi từ câu 61 đến câu 65:
Chúng ta ai cũng khao khát thành công. Tuy nhiên, mỗi người định nghĩa thành công theo cách riêng. Có người gắn thành công với sự giàu có về tiền bạc, quyền lực, tài cao học rộng; có người lại cho rằng một gia đình êm ấm, con cái nên người là thành công…Chung quy lại, có thể nói thành công là đạt được những điều mong muốn, hoàn thành mục tiêu của mình.
Nhưng nếu suy ngẫm kĩ, chúng ta sẽ nhận ra rằng thật ra, câu hỏi quan trọng không phải là “Thành công là gì?” mà là “Thành công để làm gì?”. Tại sao chúng ta lại khao khát thành công? Suy cho cùng, điều chúng ta muốn không phải bản thân ta thành công mà là cảm giác mãn nguyện và dễ chịu mà thành công đem lại, khi chúng ta đạt được mục tiêu của mình. Chúng ta nghĩ rằng đó chính là hạnh phúc. Nói cách khác, đích cuối cùng mà chúng ta nhắm tới là hạnh phúc, còn thành công chỉ là phương tiện.
Quan niệm cho rằng thành công sẽ giúp chúng ta hạnh phúc hơn chỉ là sự ngộ nhận, ảo tưởng.
Bạn hãy để hạnh phúc trở thành nền tảng cuộc sống, là khởi nguồn giúp bạn thành công hơn chứ không phải điều ngược lại. Đó chính là “bí quyết” để bạn có một cuộc sống thực sự thành công.
(Theo Lê Minh, http://songhanhphuc.net)
Đáp án A
Phương pháp giải:
Căn cứ 6 phương thức biểu đạt đã học (miêu tả, tự sự, biểu cảm, nghị luận, thuyết minh, hành chính – công vụ).
Giải chi tiết:
Phương thức biểu đạt chính: nghị luận.
Câu 62:
Theo tác giả, thành công là gì?
Đáp án A
Phương pháp giải:
Đọc, tìm ý
Giải chi tiết:
Thành công là đạt được những điều mong muốn, hoàn thành mục tiêu của mình.
Câu 63:
Theo tác giả, đích cuối cùng mà chúng ta nhắm tới là gì?
Đáp án A
Phương pháp giải:
Đọc, tìm ý
Giải chi tiết:
Đích cuối cùng mà chúng ta nhắm tới là hạnh phúc.
Câu 64:
Xác định biện pháp tu từ trong câu văn sau: “Có người gắn thành công với sự giàu có về tiền bạc, quyền lực, tài cao học rộng; có người lại cho rằng một gia đình êm ấm, con cái nên người là thành công…”
Đáp án C
Phương pháp giải:
Căn cứ các biện pháp tu từ đã học
Giải chi tiết:
Biện pháp: liệt kê: tiền bạc, quyền lực, tài cao học rộng, gia đình êm ấm.
Câu 65:
Đáp án A
Phương pháp giải:
Phân tích, tổng hợp
Giải chi tiết:
Bài học: Bí quyết để có cuộc sống thành công thực sự
Câu 66:
Đọc đoạn trích sau và thực hiện các câu hỏi từ câu 66 đến câu 70:
“Có một chiếc đồng hồ điện ở Versailles, Paris, được làm từ 1746 mà đến nay vẫn tiện dụng và hợp thời, đúng nửa đêm 31/12/1999, nó đã gióng chuông và chuyển con số 1 (đeo đuổi trên hai trăm năm) thành con số 2, kèm theo ba số không. Và, “theo tính toán hiện nay, chiếc đồng hồ này còn tiếp tục báo năm báo tháng báo giờ… nghiêm chỉnh thêm năm trăm năm nữa”.
Sở dĩ người xưa làm được việc đó, vì họ luôn luôn hướng về một cái gì trường tồn. Duy cái điều có người liên hệ thêm “còn ngày nay, người ta chỉ chăm chăm xây dựng một tòa nhà dùng độ 20 năm rồi lại phá ra làm cái mới” thì cần dừng lại kỹ hơn một chút.
Nếu người ta nói ở đây là chung cho con người thế kỷ XX thì nói thế là đủ. Một đặc điểm của kiểu tư duy hiện đại là nhanh, hoạt, không tính quá xa, vì biết rằng mọi thứ nhanh chóng lạc hậu. Nhưng cái gì có thể trường tồn được thì họ vẫn làm theo kiểu trường tồn. Chính việc sẵn sàng chấp nhận mọi thay đổi chứng tỏ sự tính xa của họ.
Riêng ở ta, phải nói thêm: trong tình trạng kém phát triển của khoa học và công nghệ một số người cũng thích nói tới hiện đại. Nhưng trong phần lớn trường hợp đó là một sự hiện đại học đòi méo mó, nó hiện ra thành cách nghĩ thiển cận và vụ lợi.
Không phải những người tuyên bố “hãy làm đi, đừng nghĩ ngợi gì nhiều, bác bỏ sự nghĩ hoàn toàn. Có điều ở đây, bộ máy suy nghĩ bị đặt trong tình trạng tự phát, người trong cuộc như tự cho phép mình “được đến đâu hay đến đấy” “không cần xem xét và đối chiếu với mục tiêu lâu dài rồi tính toán cho mệt óc, chỉ cần có những giải pháp tạm thời, cốt đạt được những kết quả rõ rệt ai cũng trông thấy là đủ”. Bấy nhiêu yếu tố gộp lại làm nên sự hấp dẫn đặc biệt của lối suy nghĩ thiển cận, vụ lợi và người ta cứ tự nhiên mà sa vào đó lúc nào không biết”
(Vương Trí Nhàn – Nhân nào quả ấy, NXB Phụ nữ, 2005, tr.93 – 94)
Phương thức biểu đạt chính được sử dụng trong đoạn trích trên là gì?
Đáp án D
Phương pháp giải:
Căn cứ 6 phương thức biểu đạt đã học (miêu tả, tự sự, biểu cảm, nghị luận, thuyết minh, hành chính – công vụ).
Giải chi tiết:
Phương thức biểu đạt chính: nghị luận
Câu 67:
Theo tác giả bài viết trên, nguyên nhân nào khiến người xưa tạo nên được những sản phẩm giống như cái chiếc đồng hồ ở điện Versailles?
Đáp án A
Phương pháp giải:
Đọc, tìm ý
Giải chi tiết:
Theo tác giả bài viết trên, nguyên nhân khiến người xưa tạo nên được những sản phẩm giống như cái chiếc đồng hồ ở điện Versailles: Người xưa luôn hướng về sự trường tồn
Câu 68:
Theo tác giả, đâu là đặc điểm của kiểu tư duy hiện đại?
Đáp án A
Phương pháp giải:
Đọc, tìm ý
Giải chi tiết:
Theo tác giả, đặc điểm của kiểu tư duy hiện đại: nhanh, hoạt, không tính quá xa
Câu 69:
Tại sao tác giả không tán đồng với một số người “ở ta” khi họ “thích nói tới hiện đại”?
Đáp án B
Phương pháp giải:
Đọc, tìm ý
Giải chi tiết:
Tác giả không tán đồng với một số người “ở ta” khi họ “thích nói tới hiện đại” vì: phần lớn trường hợp đó là một sự hiện đại học đòi méo mó, nó hiện ra thành cách nghĩ thiển cận và vụ lợi.
Câu 70:
Thông điệp được rút ra từ đoạn trích?
Đáp án C
Phương pháp giải:
Phân tích, tổng hợp
Giải chi tiết:
Thông điệp rút ra từ đoạn trích: Cần phân biệt thói thiển cận và đầu óc thực tế
Câu 71:
Xác định một từ/cụm từ SAI về ngữ pháp/hoặc ngữ nghĩa/logic/phong cách.
“Sống trong các môi trường khác nhau, trải qua quá trình lâu dài, cây xanh đã hình thành một số đặc tính thích nghi.”
Đáp án C
Phương pháp giải:
Căn cứ bài Chữa lỗi dùng từ
Giải chi tiết:
- Đặc tính là cụm từ dùng để chỉ những tính chất chỉ có ở một cá thể.Ở đây câu văn muốn nói đến cây xanh nói chung nên sử dụng từ đặc tính là không phù hợp. Thay vào đó nên dùng cụm từ “đặc điểm” sẽ phù hợp hơn.
Câu 72:
Xác định một từ/cụm từ SAI về ngữ pháp/hoặc ngữ nghĩa/logic/phong cách.
Ý tưởng nghệ thuật không bao giờ là tri thức trừu tượng một mình trên cao. Một câu thơ, một trang truyện, một vở kịch, cho đến một bức tranh, một bản đàn, ngay cả khi làm chúng ta rung động trong cảm xúc, có bao giờ để trí óc chúng ta năm lười yên một chỗ.
Đáp án A
Phương pháp giải:
Căn cứ bài Chữa lỗi dùng từ
Giải chi tiết:
Sử dụng từ “ý tưởng” trong câu văn này là không hợp lý. Bởi lẽ: “ý tưởng” là từ dùng để những suy nghĩ chưa hoàn thiện. => Sửa lại: Tư tưởng (quan niệm, suy nghĩ về một vấn đề nào đó).
Câu 73:
Xác định một từ/cụm từ SAI về ngữ pháp/hoặc ngữ nghĩa/logic/phong cách.
“Việt Bắc trước hết là một bài thơ trữ tình… Bài thơ là khúc hát ân tình thủy chung réo rắt, đằm thắm bậc nhất, và chính điều đó làm nên sức ngân vang sâu thẳm, lâu bền của bài thơ.”Đáp án A
Phương pháp giải:
Căn cứ vào hiểu biết về bài Việt Bắc
Giải chi tiết:
Việt Bắc được biết đến không chỉ là một bài thơ trữ tình
=> Sửa lại: Việt Bắc trước hết là một bài thơ trữ tình – chính trị… Bài thơ là khúc hát ân tình thủy chung réo rắt, đằm thắm bậc nhất, và chính điều đó làm nên sức ngân vang sâu thẳm, lâu bền của bài thơ
Câu 74:
Xác định một từ/cụm từ SAI về ngữ pháp/hoặc ngữ nghĩa/logic/phong cách.
Gốm thời Lê thừa hưởng những tinh hoa của Gốm thời Lý, Trần. Phát triển được nhiều loại men quý hiếm như: Men ngọc, hoa nâu, men trắng, men xanh… đề tài trang trí rất phong phú mang đậm nét dân gian hơn nét cung đình.
Đáp án A
Phương pháp giải:
Căn cứ vào nghĩa của từ
Giải chi tiết:
“thừa hưởng” là cụm từ để chỉ việc được hưởng lợi ích từ người đi trước một cách trọn vẹn không phát triển thêm. Sử dụng cụm từ này ở đây không phù hợp.
Câu 75:
Xác định một từ/cụm từ SAI về ngữ pháp/hoặc ngữ nghĩa/logic/phong cách.
Nguyễn Tuân đã sáng tạo ra một con Sông Đà không phải là thiên nhiên vô tri, vô giác, mà là một sinh thể có hoạt động, có tính cách, cá tính, có tâm trạng hẳn hoi và khá phức tạp. Nó có hai nét tính cách cơ bản song song nhau như tác giả nói – “hung bạo và trữ tình.
Đáp án D
Phương pháp giải:
Căn cứ vào nghĩa của từ.
Giải chi tiết:
Hai nét tính các của con sông Đà là hai nét tính cách trái ngược vì thế dùng từ “song song” là không hợp lý
=> Sửa lại: Nguyễn Tuân đã sáng tạo ra một con Sông Đà không phải là thiên nhiên vô tri, vô giác, mà là một sinh thể có hoạt động, có tính cách, cá tính, có tâm trạng hẳn hoi và khá phức tạp. Nó có hai nét tính cách cơ bản đối lập nhau như tác giả nói – “hung bạo và trữ tình
Câu 76:
Chọn một từ mà nghĩa của nó KHÔNG cùng nhóm với các từ còn lại.
Đáp án C
Phương pháp giải:
Vận dụng kiến thức về nghĩa của từ
Giải chi tiết:
Các từ: giáo viên, giảng viên, nghiên cứu sinh đều là các từ chỉ chức danh, tên gọi ngành nghề (danh từ)
Từ “ nghiên cứu” để chỉ hành động (động từ)
Câu 77:
Chọn một từ mà nghĩa của nó KHÔNG cùng nhóm với các từ còn lại.
Đáp án C
Phương pháp giải:
Vận dụng kiến thức về tính từ
Giải chi tiết:
Các từ “vui vẻ”, “vui tươi”, “hạnh phúc” là những từ chỉ trạng thái
Từ “vui chơi” chỉ hoạt động.
Câu 78:
Chọn một từ mà nghĩa của nó KHÔNG cùng nhóm với các từ còn lại.
Đáp án D
Phương pháp giải:
Căn cứ vào các loại từ đã học
Giải chi tiết:
Các từ: “kiến thiết”, “xây dựng”, “tu sửa” dùng đối với các công trình lớn. Riêng từ “sửa chữa” dùng cho các đồ vật nhỏ hàng ngày.
Câu 79:
Đáp án C
Phương pháp giải:
Căn cứ vào hiểu biết về các tác giả đã học trong chương trình THPT
Giải chi tiết:
Quang Dũng sáng tác vào giai đoạn kháng chiến chống Pháp. Còn lại các nhà văn, nhà thơ khác đều thuộc thế hệ sau 1975.
Câu 80:
Đáp án A
Phương pháp giải:
Vận dụng những hiểu biết về các tác phẩm trong phong trào thơ mới.
Giải chi tiết:
Hai đứa trẻ là tác phẩm truyện ngắn trữ tình của tác giả Thạch Lam. Đặc trưng của thể loại này là các tác phẩm thường không có cốt truyện hoặc cốt truyện mờ nhạt nhưng lại đi sâu vào việc phân tích diễn biến tâm lý nhân vật.
Câu 81:
Chọn từ/cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
“Tây Tiến – sự thăng hoa của một tâm hồn ________”
Đáp án B
Phương pháp giải:
Căn cứ hiểu biết về tác phẩm Tây Tiến và hồn thơ Quang Dũng
Giải chi tiết:
Tây Tiến – sự thăng hoa của một tâm hồn lãng mạn
Câu 82:
Chọn từ/cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
“Điều quan trọng hơn hết trong sự nghiệp của những nhà văn vĩ đại ấy lại là cuộc sống, trường đại học chân chính của thiên tài. Họ đã biết đời sống xã hội của thời đại, đã cảm thấy sâu sắc mọi nỗi đau đớn của con người trong thời đại, đã __________ tận đáy tâm hồn với những nỗi lo âu, bực bội, tủi hổ và những ước mong tha thiết nhất của loài người.”
Đáp án C
Phương pháp giải:
Căn cứ vào ý nghĩa từ và câu
Giải chi tiết:
Điều quan trọng hơn hết trong sự nghiệp của những nhà văn vĩ đại ấy lại là cuộc sống, trường đại học chân chính của thiên tài. Họ đã biết đời sống xã hội của thời đại, đã cảm thấy sâu sắc mọi nỗi đau đớn của con người trong thời đại, đã rung động tận đáy tâm hồn với những nỗi lo âu, bực bội, tủi hổ và những ước mong tha thiết nhất của loài người.
Câu 83:
Chọn từ/cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Tài nguyên động vật tài nguyên chung, có vai trò quyết định tới sự ___________ bền vững của đất nước chúng ta
Đáp án B
Phương pháp giải:
Căn cứ vào ý nghĩa từ và câu
Giải chi tiết:
Tài nguyên động vật tài nguyên chung, có vai trò quyết định tới sự phát triển bền vững của đất nước chúng ta.
Câu 84:
Chọn từ/cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Nguyễn Khuyến là nhà thơ của thời đại _______ sâu sắc về tư tưởng và văn hóa, khi Nho học đã tỏ ra _____ trước sự nghiệp cứu nước.
Đáp án A
Phương pháp giải:
Căn cứ vào nội dung câu văn.
Giải chi tiết:
Nguyễn Khuyến là nhà thơ của thời đại khủng hoảng sâu sắc về tư tưởng và văn hóa, khi Nho học đã tỏ ra bất lực trước sự nghiệp cứu nước.
Câu 85:
Chọn từ/cụm từ thích hợp nhất để điền vào chỗ trống trong câu dưới đây:
Cụ ngửa cổ ra đằng sau, uống một hơi _______, rồi vừa chép miệng vừa lần ruột tượng trả tiền. Cụ để ba đồng xu vào tay Liên, xoa đầu chị một cái rồi ______ bước ra ngoài.
Đáp án C
Phương pháp giải:
Căn cứ vào nội dung câu văn.
Giải chi tiết:
Cụ ngửa cổ ra đằng sau, uống một hơi cạn sạch, rồi vừa chép miệng vừa lần ruột tượng trả tiền. Cụ để ba đồng xu vào tay Liên, xoa đầu chị một cái rồi lảo đảo bước ra ngoài.
Câu 86:
Đọc đoạn trích sau đây và trả lời câu hỏi:
“Lúc ấy đã khuya. Trong nhà ngủ yên. Mị trở dậy thổi lửa, ngọn lửa bập bùng sáng lên. Mị trông sang thấy hai mắt A Phủ cũng vừa mở. Dòng nước mắt lấp lánh bò xuống hai hõm má đã xám đen. Thấy tình cảnh thế, Mị chợt nhớ đêm năm trước, A Sử trói Mị, Mị cũng phải trói đứng thế kia. Nước mắt chảy xuống miệng, xuống cổ, không biết lau đi được. Trời ơi nó bắt trói đứng người ta đến chết. Nó bắt mình chết cũng thôi. Nó đã bắt trói đến chết người đàn bà ngày trước ở cái nhà này. Chúng nó thật độc ác. Chỉ đêm mai là người kia chết, chết đau, chết đói, chết rét, phải chết. Ta là thân đàn bà, nó đã bắt về trình ma rồi, chỉ còn biết đợi ngày rũ xương ở đây thôi... Người kia việc gì mà phải chết. A Phủ... Mị phảng phất nghĩ như vậy..”
(Trích “Vợ chồng A Phủ” – Tô Hoài, SGK Ngữ văn 12 tập 2, NXBGD năm 2014)
Hình ảnh sợi dây trói trong đoạn trích trên có ý nghĩa gì?
Đáp án D
Phương pháp giải:
Căn cứ vào nội dung đoạn trích
Giải chi tiết:
Hình ảnh sợi dây trói là một hình ảnh đại diện cho chế độ cường quyền (sự áp bức bóc lột của thực dân phong kiến với đại diện là cha con nhà thống lý Patra), thần quyền và nam quyền đã trói buộc cuộc đời của những người dân nghèo khốn khổ như Mị và A Phủ.
Câu 87:
Bà lão khẽ thở dài đứng lên, đăm đăm nhìn người đàn bà. Thị cúi mặt xuống, tay vân vê tà áo đã rách bợt. Bà lão nhìn thị và bà nghĩ: Người ta có gặp bước khó khăn, đói khổ này, người ta mới lấy đến con mình. Mà con mình mới có vợ được... Thôi thì bổn phận bà là mẹ, bà đã chẳng lo lắng được cho con... May ra mà qua khỏi được cái tao đoạn này thì thằng con bà cũng có vợ, nó yên bề nó, chẳng may ra ông giời bắt chết cũng phải chịu chứ biết thế nào mà lo cho hết được?
(Trích đoạn trích Vợ nhặt, Kim Lân, SGK Ngữ văn lớp 12, tập 2)
Đoạn trích trên thể hiện phẩm chất gì của bà cụ Tứ?
Đáp án A
Phương pháp giải:
Căn cứ vào nội dung đoạn trích
Giải chi tiết:
Đoạn trích thể hiện phẩm chất tốt đẹp của bà cụ Tứ. Đó là một người mẹ yêu con. Bà thừa hiểu mục đích thị đồng ý lấy Tràng là để kiếm miếng ăn chứ không hề xuất phát từ tình yêu. Hơn nữa trong hoàn cảnh nạn đói bà hoàn toàn có thể không chấp nhận thị. Thế nhưng bà vẫn bằng lòng bởi bà nghĩ nhờ có thế mà con bà mới có vợ và bà cảm thấy vui vì điều này.Câu 88:
Đọc đoạn trích sau đây và trả lời các câu hỏi:
Con Sông Đà tuôn dài tuôn dài như một áng tóc trữ tình, đầu tóc chân tóc ẩn hiện trong mây trời tây Bắc bung nở hoa ban hoa gạo tháng hai va cuồn cuộn mù khói Mèo đốt nương xuân. Tôi đã nhìn say sưa làn mây mùa xuân bay trên Sông Đà, tôi đã xuyên qua đám mây mùa thu mà nhìn xuống dòng nước Sông Đà. Mùa xuân dòng xanh ngọc bích, chứ nước Sông Đà không xanh màu xanh canh hến của Sông Gâm Sông Lô. Mùa thu nước Sông đà lừ lừ chín đỏ như da mặt một người bầm đi vì rượu bữa, lừ lừ cái màu đỏ giận dữ ở một người bất mãn bực bội gì mỗi độ thu về. Chưa hề bao giờ tôi thấy dòng Sông Đà là đen như thực dân Pháp đã đè ngửa con sông ta ra đổ mực Tây vào mà gọi bằng một cái tên Tây láo lếu, rồi cứ thế mà phiết vào bản đồ lai chữ.
(Trích Người lái đò Sông Đà – Nguyễn Tuân, Ngữ văn 12, Tập một, NXB Giáo dục)
Đoạn trích trên nói đến vẻ đẹp nào của con Sông Đà?
Đáp án B
Phương pháp giải:
Căn cứ vào nội dung đoạn trích
Giải chi tiết:
Đoạn trích trên thể hiện vẻ đẹp trữ tình của con Sông Đà ở khúc sông hạ nguồn.
Câu 89:
Đọc đoạn trích sau đây và trả lời các câu hỏi:
Trống cầm canh ở huyện đánh tung lên một tiếng ngắn, khô khan, không vang động ra xa, rồi chìm ngay vào bóng tối. Người vắng mãi, trên hàng ghế chị Tí mới có hai ba bác phu ngồi uống nước và hút thuốc lào. Nhưng một lát từ phố huyện đi ra, hai ba người cầm đèn lồng lung lay các bóng dài: mấy người làm công ở hiệu khách đi đón bà chủ ở tỉnh về. Bác Siêu nghển cổ nhìn ra phía ga, lên tiếng:
- Đèn ghi đã ra kia rồi.
Liên cũng trông thấy ngọn lửa xanh biếc, sát mặt đất, như ma trơi. Rồi tiếng còi xe lửa ở đâu vang lại, trong đêm khuya kéo dài ra theo gió xa xôi. Liên đánh thức em:
- Dậy đi, An. Tàu đến rồi.
(Trích Hai đứa trẻ – Thạch Lam, Ngữ văn 11, Tập hai, NXB Giáo dục)
Hình ảnh đoàn tàu được nhắc đến trong đoạn trích thể hiện điều gì?
Đáp án B
Phương pháp giải:
Căn cứ vào nội dung đoạn trích
Giải chi tiết:
Hình ảnh đoàn tàu được nhắc đến trong đoạn trích thể hiện cho những ước muốn khiêm nhường mà nhỏ bé của người dân nghèo nơi phố huyện. Họ muốn thấy một cái gì đó rộn ràng hơn khác với cuộc sống tối tăm cũng như mong muốn một sự thay đổi đến với cuộc đời mình.
Câu 90:
Đọc đoạn trích sau đây và trả lời các câu hỏi:
“Tương tư thức mấy đêm rồi
Biết cho ai hỏi, ai người biết cho
Bao giờ bến mới gặp đò
Hoa khuê các bướm giang hồ gặp nhau”
(Tương tư – Nguyễn Bính, Ngữ văn 11, Tập hai, NXB Giáo dục)
Câu thơ “Bao giờ bến mới gặp đò” sử dụng biện pháp tu từ nào?
Đáp án D
Phương pháp giải:
Căn cứ vào nội dung đoạn trích
Giải chi tiết:
Câu thơ “Bao giờ bến mới gặp đò” sử dụng biện pháp tu từ ẩn dụ. Trong đó “bến” là hình ảnh ẩn dụ cho người con gái, “đò” là hình ảnh ẩn dụ cho người con trai.
Câu 91:
Đọc đoạn trích sau đây và trả lời các câu hỏi:
Ông Huấn Cao lặng nghĩ một lát rồi mỉm cười: “Về bảo với chủ ngươi, tối nay, lúc nào lính canh về trại nghỉ, thì đem lụa, mực, bút và một bó đuốc xuống đây ta cho chữ. Chữ thì quý thực. Ta nhất sinh không vì vàng ngọc hay quyền thế mà ép mình viết câu đối bao giờ. Đời ta cũng mới viết có hai bộ tứ bình và một bức trung đường cho ba người bạn thân của ta thôi. Ta cảm cái tấm ông biệt nhỡn liên tài của các người. Nào ta có biết đâu một người như thầy Quản đây mà lại có những sở thích cao quý như vậy. Thiếu chút nữa, ta đã phụ mất một tấm lòng trong thiên hạ”.
(Trích Chữ người tử tù – Nguyễn Tuân, Ngữ văn 11, Tập một, NXB Giáo dục)
Câu nói của Huấn Cao trong đoạn trích trên đại diện cho phẩm chất gì của ông?
Đáp án A
Phương pháp giải:
Căn cứ nội dung đoạn trích
Giải chi tiết:
Câu nói của Huấn Cao cho thấy ông là một người có thiên lương cao đẹp. Lúc trước ông không cúi đầu, thậm chí tỏ ra ghét bỏ, coi thường quản ngục là vì nghĩ quản ngục cũng giống như bao tên quan khác là tay sai của nhà nước phong kiến. Về sau khi biết quản ngục là người có thiên lương ông đồng ý cho chữ. Như vậy có thể thấy, Huấn Cao không sợ cường quyền hay không vì vàng ngọc mà cúi đầu. Ông chỉ cúi đầu trước cái đẹp. Đó chính là biểu hiện của một con người có thiên lương cao đẹp.
Câu 92:
Đọc đoạn trích sau đây và trả lời các câu hỏi:
“Quyện điểu quy lâm tầm túc thụ
Cô vân mạn mạn độ thiên không
Sơn thôn thiếu nữ ma bao túc
Bao túc ma hoàn lô dĩ hồng”
(Chiều tối – Hồ Chí Minh, Ngữ văn 11, Tập hai, NXB Giáo dục)
Cụm từ “ma bao túc” có ý nghĩa gì?
Đáp án A
Phương pháp giải:
Căn cứ vào nội dung đoạn trích
Giải chi tiết:
Cụm từ “ma bao túc” có nghĩa là xay ngô
Câu 93:
Đọc đoạn trích sau đây và trả lời các câu hỏi:
Sáng hôm sau, đúng 7 giờ thì cất đám. Hai viên cảnh sát thuộc bộ thứ 18 là Min Ðơ và Min Toa đã được thuê giữ trật tự cho đám ma. Giữa lúc không có ai đáng phạt mà phạt, đương buồn rầu như những nhà buôn sắp vỡ nợ, mấy ông cảnh binh này được có đám thuê thì sung sướng cực điểm, đã trông nom rất hết lòng. Thành thử tang gia ai cũng vui vẻ cả, trừ một Tuyết. Tại sao Xuân lại không đến phúng viếng gì cả. Tại sao Xuân lại không đi đưa? Hay là Xuân khinh mình? Những câu hỏi ấy đã khiến Tuyết đau khổ một cách rất chính đáng, có thể muốn tự tử được. Tìm kiếm khắp mặt trong bọn người đi đưa đám ma cũng không thấy “bạn giai” đâu cả, Tuyết như bị kim châm vào lòng.
(Hạnh phúc của một tang gia – Vũ Trọng Phụng, Ngữ văn 11, Tập một, NXB Giáo dục, 2007, tr.29)
Đoạn trích trên được viết theo phương thức biểu đạt nào?
Đáp án C
Phương pháp giải:
Căn cứ vào các phương thức biểu đạt đã học
Giải chi tiết:
Đoạn trích trên được viết theo phương thức tự sự.
Câu 94:
Đọc đoạn trích sau đây và trả lời các câu hỏi:
“Lát lâu sau mụ lại mới nói tiếp:
- Mong các chú cách mạng thông cảm cho, đám đàn bà hàng chài ở thuyền chúng tôi cần phải có người đàn ông để chèo chống phong ba, để cùng làm ăn nuôi nấng đặng một sắp con, nhà nào cũng trên dưới chục đứa. Ông trời sinh ra người đàn bà là để đẻ con, rồi nuôi con cho đến khi khôn lớn cho nên phải gánh lấy cái khổ. Đàn bà ở thuyền chúng tôi phải sống cho con chứ không thể sống cho mình như ở trên đất được! Mong các chú lượng tình cho cái sự lạc hậu. Các chú đừng bắt tôi bỏ nó! - Lần đầu tiên trên khuôn mặt xấu xí của mụ chợt ửng sáng lên như một nụ cười - vả lại, ở trên chiếc thuyền cũng có lúc vợ chồng con cái chúng tôi sống hòa thuận, vui vẻ.”
(Trích Chiếc thuyền ngoài xa – Nguyễn Minh Châu, Ngữ văn 12, Tập hai, NXB Giáo dục)
Đoạn trích trên được kể thông qua lời của ai?
Đáp án D
Phương pháp giải:
Căn cứ vào nội dung văn bản đã học
Giải chi tiết:
Đoạn trích được kể thông qua lời của nhân vật Phùng.
Câu 95:
Đọc đoạn trích sau đây và trả lời các câu hỏi:
“Sao anh không về chơi thôn Vĩ?
Nhìn nắng hàng cau nắng mới lên
Vườn ai mướt quá xanh như ngọc
Lá trúc che ngang mặt chữ điền”
(Trích Đây thôn Vĩ Dạ – Hàn Mặc Tử, Ngữ văn 11, Tập hai, NXB Giáo dục)
Dòng nào dưới đây nêu đúng các biện pháp tu từ được sử dụng?
Phương pháp giải:
Căn cứ vào các biện pháp tu từ đã học.
Giải chi tiết:
Đoạn thơ trên sử dụng các biện pháp tu từ:
- Câu hỏi tu từ (Sao anh không về chơi thôn Vĩ?)
- Điệp từ (Nắng)
- So sánh (Màu xanh của khu vườn được so sánh với viên ngọc)Câu 96:
Đọc đoạn trích sau đây và trả lời các câu hỏi:
Xuân đương tới nghĩa là xuân đương qua
Xuân còn non nghĩa là xuân sẽ già
Mà xuân hết nghĩa là tôi cũng mất
Lòng tôi rộng nhưng lượng trời cứ chật
Không cho dài thời trẻ của nhân gian.
(Vội vàng – Xuân Diệu, Ngữ văn 11, Tập hai, NXB Giáo dục)
Dòng nào dưới đây nêu đúng nhất nội dung đoạn trích trên:
Đáp án B
Phương pháp giải:
Vận dụng kiến thức đã học trong bài Vội vàng
Giải chi tiết:
Đoạn thơ này thể hiện quan niệm mới mẻ của tác giả về mua xuân, tuổi trẻ và tình yêu.
Câu 97:
Đọc đoạn trích sau đây và trả lời các câu hỏi:
Hắn lắc đầu:
- Không được! Ai cho tao lương thiện? Làm thế nào cho mất được những vết mảnh chai trên mặt này? Tao không thể là người lương thiện nữa. Biết không? Chỉ có một cách... biết không! Chỉ có một cách là... cái này biết không?
Hắn rút dao ra xông vào. Bá Kiến ngồi nhỏm dậy, Chí Phèo đã văng dao tới rồi. Bá Kiến chỉ kịp kêu một tiếng. Chí Phèo vừa chém túi bụi vừa kêu làng thật to. Hắn kêu làng, không bao giờ người ta vội đến. Bởi thế khi người ta đến thì hắn cũng đang giẫy đành đạch ở giữa bao nhiêu là máu tươi. Mắt hắn trợn ngược. Mồm hắn ngáp ngáp, muốn nói, nhưng không ra tiếng. Ở cổ hắn, thỉnh thoảng máu vẫn còn ứ ra.
(Trích “Chí Phèo” – Nam Cao, Ngữ văn 11, Tập một, NXB Giáo dục)
Dòng nào dưới đây gọi đúng nhất giọng điệu và thái độ của Chí Phèo khi đối chất với Bá Kiến?
Đáp án D
Phương pháp giải:
Căn cứ vào tác phẩm Chí Phèo.
Giải chi tiết:
Giọng điệu của Chí Phèo trong đoạn trích trên thể hiện sự căm phẫn, tuyệt vọng. Căm phẫn vì bị chế độ áp bức đẩy đến bước đường cùng, tuyệt vọng vì bị cự tuyệt quyền làm người. Hắn không thể quay trở về thế giới bằng phẳng của những người lương thiện được nữa.
Câu 98:
Đọc đoạn trích sau đây và trả lời các câu hỏi:
Đan Thiềm (thất vọng): - Chỉ tại ông không nghe tôi, dùng dằng mãi. Bây giờ… (Nói với Ngô Hạch) Xin tướng quân…
Ngô Hạch: Dẫn nó đi, không cho nó nói nhảm nữa, rờm tai (quân sĩ dẫn nàng ra)
Đan Thiềm: Ông Cả! Đài lớn tan tành! Ông Cả ơi! Xin cùng ông vĩnh biệt! (Họ kéo nàng ra tàn nhẫn)
(Trích Vĩnh biệt Cửu Trùng Đài – Nguyễn Huy Tưởng, Ngữ văn 11, Tập một, NXB Giáo dục)
Trong những câu cuối cùng của mình, Đan Thiềm đã bái biệt Vũ Như Tô và cầu xin cùng ông vĩnh biệt điều gì?
Đáp án C
Phương pháp giải:
Căn cứ vào nội dung của tác phẩm Vĩnh biệt Cửu Trùng Đài.
Giải chi tiết:
Đài Cửu Trùng chính là hình ảnh thể hiện mộng lớn của Vũ Như Tô và Đan Thiềm. Đài Cửu Trùng cháy có nghĩa là mộng lớn đã tan thành mây khói. Đan Thiềm nói vĩnh biệt ở đây là vĩnh biệt mộng lớn của hai người.
Câu 99:
Đọc đoạn trích sau đây và trả lời các câu hỏi:
Rời khỏi kinh thành, sông Hương chếch về hướng chính bắc, ôm lấy đảo Cồn Hến quanh năm mơ màng trong sương khói, đang xa dần thành phố để lưu luyến ra đi giữa màu xanh của tre trúc và của những vườn cau vùng ngoại ô Vĩ Dạ. Và rồi, như sực nhớ lại một điều gì chưa kịp nói, nó đột ngột đổi dòng, rẽ ngoặt sang hướng đông tây để gặp lại thành phố lần cuối ở góc thị trấn Bao Vinh xưa cổ. Đối với Huế, nơi đây chính là chỗ chia tay dõi xa ngoài mười dặm trường đình.
(Trích Ai đã đặt tên cho dòng sông – Hoàng Phủ Ngọc Tường, Ngữ văn 12, Tập một, NXB Giáo dục)
Vẻ đẹp của con sông Hương được tác giả miêu tả dưới góc nhìn nào?Đáp án A
Phương pháp giải:
Căn cứ vào nội dung của tác phẩm
Giải chi tiết:
Vẻ đẹp con sông Hương trong đoạn trích trên được cảm nhận dưới góc nhìn địa ý.
Câu 100:
Đọc đoạn trích sau đây và trả lời các câu hỏi:
Việt muốn chạy thật nhanh, thoát khỏi sự vắng lặng này, về với ánh sáng ban ngày, gặp lại anh Tánh, níu chặt lấy các anh mà khóc như thằng Út em vẫn níu chân chị Chiến, nhưng chân tay không nhấc lên được. Bóng đêm vắng lặng và lạnh lẽo bao trùm lấy Việt, kéo theo đến cả con ma cụt đầu vẫn ngồi trên cây xoài mồ côi và thằng chỏng thụt lưỡi hay nhảy nhót trong những đêm mưa ngoài vàm sông, cái mà Việt vẫn nghe các chị nói hồi ở nhà, Việt nằm thở dốc...
(Trích đoạn trích Những đứa con trong một gia đình, Nguyễn Thi, SGK Ngữ văn lớp 12 tập 2)
Đoạn văn trên nói đến phẩm chất gì của nhân vật Việt?
Đáp án C
Phương pháp giải:
Căn cứ vào nội dung của đoạn trích.
Giải chi tiết:
Đoạn trích trên nói đến hình ảnh của Việt với nỗi sợ của một chàng thanh niên mới lớn.
Câu 101:
Tính chất của Chiến tranh thế giới thứ nhất (1914 - 1918) là:
Đáp án D
Phương pháp giải:
Dựa vào mục đích của các nước tham gia chiến tranh và hậu quả của cuộc chiến tranh này để đánh giá tính chất.
Giải chi tiết:
Chiến tranh thế giới thứ nhất là cuộc chiến tranh đế quốc phi nghĩa vì nổ ra do các nước đế quốc muốn tranh giành thị trường, thuộc địa. Hậu quả mà cuộc chiến tranh thế giới này để lại cho nhân loại là vô cùng nặng nề cả về vật chất và tinh thần.
Câu 102:
Nội dung nào không phải là nguyên nhân thất bại của cuộc kháng chiến chống thực dân Pháp xâm lược ở Việt Nam (1858 - 1884)?
Đáp án B
Phương pháp giải:
phân tích, suy luận.
Giải chi tiết:
Trong cuộc kháng chiến chống thực dân Pháp ở Việt Nam từ năm 1858 đến năm 1884:
- Phương án A, C: triều đình nặng về phòng thủ (xây dựng đại đồn Chí Hòa) và lần lượt kí các Hiệp ước đầu hàng thực dân Pháp.
- Phương án B: Nhân dân từ năm 1858 đến năm 1884 luôn kiên quyết đấu tranh chống Pháp, mặc dù từ Hiệp ước Nhâm Tuất (1862), triều đình đã ra lệnh giải tán các toán nghĩa binh chống Pháp.
- Phương án D: Nhân dân từ sau năm 1862 đến năm 1884 đã kết hợp chống triều đình và chống phong kiến đầu hàng.
Câu 103:
Điểm giống nhau giữa Cương lĩnh chính trị (đầu năm 1930) và Luận cương chính trị (tháng 10 năm 1930) là việc xác định
Đáp án D
Phương pháp giải:
Phân tích các phương án.
Giải chi tiết:
A loại vì nhiệm vụ được đề ra trong Cương lĩnh chính trị (đầu năm 1930) và Luận cương chính trị (10/1930) là khác nhau. Cụ thể:
- Nhiệm vụ cách mạng được nêu trong Cương lĩnh chính trị là tiến hành cách mạng tư sản dân quyền và thổ địa cách mạng để đi tới xã hội cộng sản, trong đó, đề cao vấn đề giải phóng dân tộc.
- Nhiệm vụ của Luận cương chính trị lại nêu nhiệm vụ của cách mạng là đánh đổ phong kiến và đánh đổ đế quốc, trong đó, vấn đề giai cấp được nêu cao hơn (đây là hạn chế của Luận cương).
B, C loại vì lực lượng cách mạng/động lực cách mạng được xác định trong Cương lĩnh là công nhân, nông dân, trí thức, tiểu tư sản (là các lực lượng nòng cốt) còn phú nông, trung tiểu địa chủ thì cần phải lợi dung hoặc trung lập. Luận cương chính trị chỉ xác định lực lượng/động lực cách mạng là công nhân và nông dân (hạn chế).
D chọn vì lãnh đạo cách mạng được xác định trong Cương lĩnh và Luận cương đều là công nhân với đội tiên phong là Đảng Cộng sản.
Câu 104:
Việc tách Đảng Cộng sản Đông Dương để thành lập Đảng Mác - Lênin riêng ở mỗi nước Việt Nam, Lào, Campuchia được quyết định tại
Đáp án A
Phương pháp giải:
SGK Lịch sử 12, trang 140.
Giải chi tiết:
Việc tách Đảng Cộng sản Đông Dương để thành lập Đảng Mác - Lênin riêng ở mỗi nước Việt Nam, Lào, Campuchia được quyết định tại Đại hội đại biểu lần thứ II của Đảng (2 - 1951).
Câu 105:
Năm 1919, Nguyễn Ái Quốc gửi đến Hội nghị Vécxai Bản yêu sách của nhân dân An Nam đòi Chính phủ Pháp thừa nhận quyền
Đáp án A
Phương pháp giải:
SGK Lịch sử 12, trang 81.
Giải chi tiết:
Năm 1919, Nguyễn Ái Quốc gửi đến Hội nghị Vécxai Bản yêu sách của nhân dân An Nam đòi Chính phủ Pháp thừa nhận quyền tự do, dân chủ, quyền bình đẳng và quyền tự quyết của dân tộc Việt Nam.
Câu 106:
Việc ký Hiệp định Sơ Bộ (6/3/1946) tạm hòa với Pháp chứng tỏ:
Đáp án A
Phương pháp giải:
Phân tích các phương án.
Giải chi tiết:
A chọn vì lúc này Pháp và quân Trung Hoa Dân quốc đã kí Hiệp ước Hoa – Pháp, để tránh 1 lúc phải đối phó với nhiều kẻ thù thì Đảng và Chính phủ ta đã rất linh hoạt và đúng đắn khi kí kết Hiệp định Sơ bộ với Pháp. Với Hiệp định này, ta vừa đuổi được 20 vạn quân Trung Hoa Dân quốc về nước, vừa tranh thủ được thời gian hòa hoãn để chuẩn bị cho cuộc kháng chiến về sau.
B loại vì Chính phủ ta không thỏa hiệp.
C loại vì kí Hiệp định Sơ bộ thì cả ta và Pháp đều có lợi nên không thể nói đây là thắng lợi của Pháp trên mặt trận ngoại giao.
D loại vì lúc này lực lượng cách mạng của ta không suy yếu.
Câu 107:
Đại hội lần thứ VII của Quốc tế cộng sản (tháng 7/1935) đã yêu cầu ở mỗi nước thành lập
Đáp án C
Phương pháp giải:
SGK Lịch sử 12, trang 98.
Giải chi tiết:
Đại hội lần thứ VII của Quốc tế cộng sản (tháng 7/1935) đã yêu cầu ở mỗi nước thành lập mặt trận nhân dân rộng rãi chống phát xít.
Câu 108:
Yếu tố nào tạo thời cơ khách quan thuận lợi để cách mạng tháng Tám năm 1945 ở Việt Nam diễn ra nhanh chóng và ít đổ máu?
Đáp án B
Phương pháp giải:
Suy luận, loại trừ phương án.
Giải chi tiết:
Thời cơ của cách mạng tháng Tám bao gồm nguyên nhân chủ quan và nguyên nhân khách quan. Trong đó, nội dung của các phương án A, C, D là nguyên nhân chủ quan quyết định sự thắng lợi của cách mạng tháng Tám. Còn nội dung của phương án B là nguyên nhân khách quan giúp cho cuộc cách mạng tháng Tám diễn ra nhanh chóng và ít đổ máu vì kẻ thù của ta đã suy yếu nghiêm trọng.
Câu 109:
Dựa vào thông tin dưới đây để trả lời các câu từ 109 đến 110:
Đường lối đổi mới của Đảng được đề ra lần đầu tiên tại Đại hội VI (12 – 1986), được điều chỉnh, bổ sung và phát triển tại Đại hội VII (6 - 1991), Đại hội VIII (6 – 1996), Đại hội IX (4 – 2001).
Đổi mới đất nước đi lên chủ nghĩa xã hội không phải là thay đổi mục tiêu của chủ nghĩa xã hội, mà làm cho mục tiêu ấy được thực hiện có hiệu quả bằng những quan điểm đúng đắn về chủ nghĩa xã hội, những hình thức, bước đi và biện pháp thích hợp.
Đổi mới phải toàn diện và đồng bộ, từ kinh tế và chính trị đến tổ chức, tư tưởng, văn hoá. Đổi mới kinh tế phải gắn liền với đổi mới chính trị, nhưng trọng tâm là đổi mới kinh tế.
Về đổi mới kinh tế, Đảng chủ trương xoá bỏ cơ chế quản lý kinh tế tập trung, quan liêu bao cấp, hình thành cơ chế thị trường ; xây dựng nền kinh tế quốc dân với cơ cấu nhiều ngành, nghề ; nhiều quy mô, trình độ công nghệ phát triển kinh tế hàng hoá nhiều thành phần theo định hướng xã hội chủ nghĩa ; mở rộng quan hệ kinh tế đối ngoại.
Về đổi mới chính trị, Đảng chủ trương xây dựng Nhà nước pháp quyền xã hội chủ nghĩa, Nhà nước của dân, do dân và vì dân ; xây dựng nền dân chủ xã hội chủ nghĩa, bảo đảm quyền lực thuộc về nhân dân ; thực hiện chính sách đại đoàn kết dân tộc, chính sách đối ngoại hoà bình, hữu nghị, hợp tác.
(Nguồn: SGK Lịch sử 12, trang 208 – 209).
Trong đường lối đổi mới của Việt Nam, Đảng chủ trương phát triển kinh tế hàng hóa nhiều thành phần nhằm
Đáp án C
Phương pháp giải:
Dựa vào thông tin được cung cấp để phân tích các phương án.
Giải chi tiết:
A loại vì theo nghĩa hẹp, cải tạo xã hội chủ nghĩa là tổ chức lại nền sản xuất xã hội để có năng suất lao động cao hơn.
B loại vì cho đến hiện nay tình trạng lạm phát vẫn còn.
C chọn vì thực hiện nền kinh tế hàng hóa nhiều thành phần có sự kiểm soát của nhà nước sẽ tạo ra sức mạnh tổng hợp của nền kinh tế nhiều thành phần.
D loại vì Đảng chủ trương phát triển kinh tế hàng hóa nhiều thành phần không nhằm tăng cường vai trò của thành phần kinh tế nhà nước và tập thể.
Câu 110:
Nội dung trọng tâm của đường lối đổi mới ở Việt Nam từ tháng 12 - 1986 phù hợp với xu thế phát triển của thế giới là
Đáp án A
Phương pháp giải:
Dựa vào xu thế phát triển của thế giới sau Chiến tranh lạnh và thông tin được cung cấp để suy luận.
Giải chi tiết:
- Xu thế phát triển của thế giới sau Chiến tranh lạnh là lấy phát triển kinh tế làm trọng tâm.
- Trọng tâm của đường lối đổi mới ở Việt Nam năm 1986 là đổi mới về kinh tế.Câu 111:
Đại bộ phận lãnh thổ của Liên bang Nga nằm trong vành đai khí hậu
Đáp án A
Phương pháp giải:
Kiến thức bài 8 – Liên Bang Nga (trang 63 sgk Địa 11)
Giải chi tiết:
Đại bộ phận lãnh thổ Liên Bang Nga nằm trong vành đai khí hậu ôn đới.
Câu 112:
Yếu tố vị trí địa lí và lãnh thổ giúp Nhật Bản phát triển mạnh loại hình giao thông vận tải nào sau đây?
Đáp án D
Phương pháp giải:
Liên hệ đặc điểm lãnh thổ và vị trí địa lí Nhật Bản: là đất nước quần đảo, bờ biển khúc khuỷu, kéo dài, có nhiều vũng vịnh; vị trí xung quanh đều tiếp giáp với các vùng biển thuộc Thái Bình Dương.
Giải chi tiết:
Nhật Bản là đất nước quần đảo, lãnh thổ gồm 4 đảo lớn và hàng nghìn đảo nhỏ; bờ biển khúc khuỷu, kéo dài, có nhiều vũng vịnh thuận lợi để xây dựng hệ thống các cảng biển; vị trí xung quanh đều tiếp giáp với các vùng biển thuộc Thái Bình Dương.
=> Giao thông vận tải biển đóng vai trò quan trọng đối với sự phát triển kinh tế - xã hội của vùng: tạo điều kiện để giao lưu kinh tế giữa các vùng kinh tế đảo và với các vùng kinh tế trên thế giới bằn đường biển.
=> Như vậy, yếu tố vị trí địa lí và lãnh thổ giúp Nhật Bản phát triển mạnh loại hình vận tải đường biển.
Câu 113:
Diện tích đất nông nghiệp nước ta đang giảm dần chủ yếu do
Đáp án A
Phương pháp giải:
Kiến thức bài14 – Vấn đề phát bảo vệ tài nguyên thiên nhiên
Giải chi tiết:
Đất nông nghiệp nước ta giảm do sức ép của dân số, quá trình CNH- HĐH đất nước.
Câu 114:
Đất ở đồng bằng ven biển miền Trung nước ta thường nghèo, nhiều cát do
Đáp án B
Phương pháp giải:
Liên hệ nguồn gốc hình thành đồng bằng ven biển.
Giải chi tiết:
Đất ở đồng bằng ven biển miền Trung nước ta thường nghèo, nhiều cát do nguồn gốc hình thành chủ yếu từ biển
Câu 115:
Căn cứ vào Atlat Địa lí Việt Nam trang 19, hãy xác định tỉnh có diện tích cây công nghiệp lâu năm lớn nhất ở vùng Bắc Trung Bộ?
Đáp án D
Phương pháp giải:
Sử dụng Atlat Địa lí trang 19
Giải chi tiết:
Tỉnh có diện tích cây công nghiệp lâu năm lớn nhất ở vùng Bắc Trung Bộ là Quảng Trị.
Câu 116:
Cho biểu đồ:
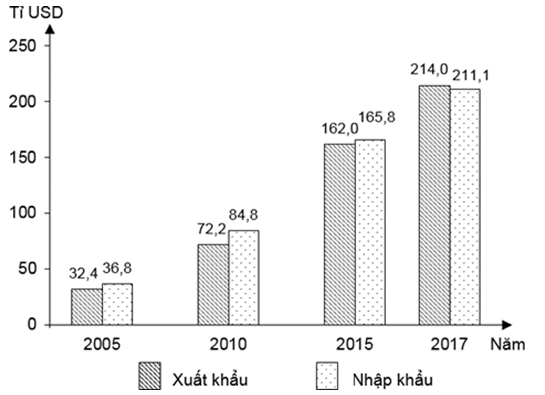
TÌNH HÌNH XUẤT, NHẬP KHẨU CỦA VIỆT NAM, GIAI ĐOẠN 2005 - 2017
(Nguồn số liệu theo Niên giám thống kê Việt Nam 2018, NXB Thống kê, 2019)
Theo biểu đồ, nhận xét nào sau đây đúng về xuất, nhập khẩu của nước ta giai đoạn 2005 - 2017?
Đáp án C
Phương pháp giải:
Kĩ năng nhận xét biểu đồ
Giải chi tiết:
- A sai: Giai đoạn 2005 – 2015 Việt Nam liên tục nhập siêu
- B sai: Xuất khẩu tăng nhiều hơn nhập khẩu (xuất khẩu tăng 181,6 tỉ USD, nhập khẩu tăng 174,3 tỉ USD)
- D sai: Năm 2017 Việt Nam xuất siêu
- C đúng: Xuất khẩu tăng nhanh hơn nhập khẩu (xuất khẩu tăng gấp 6,6 lần; nhập khẩu tăng 5,7 lần).
Câu 117:
Trong những năm qua, sản lượng lương thực của nước ta tăng lên chủ yếu là do
Đáp án D
Phương pháp giải:
Kiến thức bài 22 – Vấn đề phát triển nông nghiệp (trang 94 sgk Địa 12)
Giải chi tiết:
Trong những năm qua, sản lượng lương thực của nước ta tăng lên chủ yếu là do áp dụng rộng rãi các biện pháp thâm canh trong nông nghiệp khiến năng suất lúa tăng mạnh.
Câu 118:
Viễn thông nước ta hiện nay không phải là ngành
Đáp án B
Phương pháp giải:
SGK địa lí 12 cơ bản trang 135.
Giải chi tiết:
Viễn thông nước ta không phải là ngành chỉ phục vụ cho doanh nghiệp, mà còn phục vụ cho các hoạt động sinh hoạt, sản xuất của người dân.
Câu 119:
Việc hình thành cơ cấu kinh tế nông – lâm – ngư nghiệp có ý nghĩa lớn đối với Bắc Trung Bộ góp phần
Đáp án D
Phương pháp giải:
Kiến thức bài 35 sgk 12, trang 156-157
Giải chi tiết:
Bắc Trung Bộ có nhiều thế mạnh để phát triển kết hợp với địa hình đa dạng thay đổi từ T-D => Hình thành cơ cấu N-L-Ngư nghiệp góp phần tạo thế liên hoàn trong phát triển kinh tế từ Tây sang Đông.
Câu 120:
Để tăng vai trò trung chuyển và đẩy mạnh giao lưu theo chiều Bắc – Nam, Duyên hải Nam Trung Bộ cần phải thực hiện biện pháp chủ yếu nào sau đây?
Đáp án A
Phương pháp giải:
Kiến thức bài 36 – Vấn đề phát triển kinh tế -xã hội ở Duyên hải Nam Trung Bộ
Giải chi tiết:
Để tăng vai trò trung chuyển và đẩy mạnh giao lưu theo chiều Bắc – Nam, Duyên hải Nam Trung Bộ cần phải thực hiện các biện pháp chủ yếu là nâng cấp quốc lộ 1 và đường sắt Bắc – Nam. Bởi đây là 2 trục đường chính, kéo dài theo chiều Bắc Nam, đảm nhận vai trò vận chuyển khối lượng hàng hóa rất lớn giữa các địa phương miền Bắc và miền Trung, Nam nước ta.
Câu 121:
Đồ thị nào trong các đồ thị dưới đây có thể biểu diễn sự phụ thuộc của lực tương tác giữa hai điện tích điểm vào khoảng cách giữa chúng?
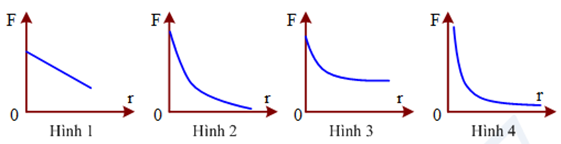
Phương pháp giải:
+ Sử dụng công thức xác định lực tương tác giữa hai điện tích điểm: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\).
+ Sử dụng lí thuyết về đồ thị hàm số.
Giải chi tiết:
Lực tương tác giữa hai điện tích điểm được xác định bởi công thức: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\).
Hay \(F = \frac{A}{{{r^2}}}\).
+ Khi \(r \to \infty \Rightarrow F \to 0\).
+ Khi \(r \to 0 \Rightarrow F \to \infty \).
\( \Rightarrow \) Đồ thị \(F\left( r \right)\) có dạng đường hypebol \( \Rightarrow \) Hình 4.
Câu 122:
Trong các hình vẽ sau, hình vẽ nào biểu diễn đúng hướng của đường cảm ứng từ của dòng điện trong dây dẫn thẳng dài vuông góc với mặt phẳng hình vẽ:
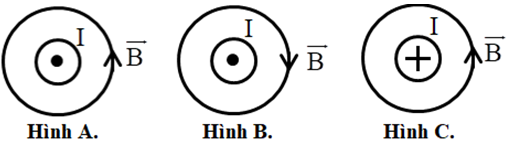
Đáp án A
Phương pháp giải:
Vận dụng quy tắc nắm tay phải để xác định chiều của cảm ứng từ : Nắm tay phải sao cho các ngón tay khum lại theo chiều dòng điện, ngón cái choãi ra \({90^0}\) chỉ chiều của cảm ứng từ.
Giải chi tiết:
Áp dụng quy tắc nắm tay phải, ta có:
Dòng điện hướng từ trong ra ngoài, từ trường hướng ngược chiều kim đồng hồ → A đúng, B sai.
Dòng điện hướng từ ngoài vào trong, từ trường hướng cùng chiều kim đồng hồ → C sai.
\( \Rightarrow \) Hình vẽ biểu diễn đúng là hình A.
Câu 123:
Một người nhìn thấy con cá ở trong nước. Hỏi muốn đâm trúng con cá thì người đó phải phóng mũi lao vào chỗ nào?
Đáp án A
Phương pháp giải:
Định luật khúc xạ ánh sáng: \({n_1}\sin i = {n_2}\sin r\).
Giải chi tiết:
Gọi O là vị trí của con cá trong nước.
Do hiện tượng khúc xạ và do chiết suất của nước lớn hơn chiết suất của không khí nên ảnh của con cá sẽ ở vị trí O’ như hình vẽ.
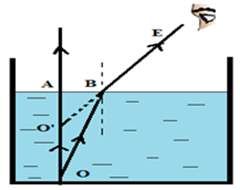
Như vậy, người đó nhìn thấy con cá dường như gần mặt nước hơn. Để đâm trúng con cá thì người đó phải phóng mũi lao vào phía dưới vị trí mà người đó nhìn thấy con cá.
Câu 124:
Một con lắc đơn dao động với biên độ \({\alpha _0} < \frac{\pi }{2}\), có mốc thế năng được chọn tại vị trí cân bằng của vật nặng. Gọi độ lớn vận tốc của vật nặng khi động năng bằng thế năng là v1, khi độ lớn của lực căng dây treo bằng trọng lực tác động lên vật là v2 . Tỉ số \(\frac{{{v_1}}}{{{v_2}}}\) có giá trị nào sau đây?
Đáp án D
Phương pháp giải:
Công thức tính độ lớn vận tốc và lực căng dây: \(\left\{ {\begin{array}{*{20}{l}}{v = \sqrt {2gl\left( {\cos \alpha - \cos {\alpha _0}} \right)} }\\{T = mg.\left( {3\cos \alpha - 2\cos {\alpha _0}} \right)}\end{array}} \right.\)
Công thức tính cơ năng, thế năng và động năng: \(\left\{ {\begin{array}{*{20}{l}}{{\rm{W}} = mgl.\left( {1 - \cos {\alpha _0}} \right)}\\{{{\rm{W}}_t} = mgl.\left( {1 - \cos \alpha } \right)}\\{{{\rm{W}}_d} = {\rm{W}} - {{\rm{W}}_t}}\end{array}} \right.\)
Theo bài ra ta có: \(\left\{ {\begin{array}{*{20}{l}}{{{\rm{W}}_t} = {{\rm{W}}_d} \Rightarrow {v_1}}\\{T = P \Rightarrow {v_2}}\end{array}} \right. \Rightarrow \frac{{{v_1}}}{{{v_2}}}\).
Giải chi tiết:
+ Khi động năng bằng thế năng: \[{{\rm{W}}_t} = {\rm{W}} - {{\rm{W}}_t}\]
\[ \Leftrightarrow mgl.\left( {1 - \cos {\alpha _1}} \right) = mgl.\left( {1 - \cos {\alpha _0}} \right) - mgl.\left( {1 - \cos {\alpha _1}} \right)\]
\[ \Leftrightarrow 1 - \cos {\alpha _1} = \cos {\alpha _1} - \cos {\alpha _0}\]
\[ \Leftrightarrow \cos {\alpha _1} = \frac{1}{2} + \frac{1}{2}.\cos {\alpha _0}\]
+ Khi độ lớn của lực căng dây treo bằng trọng lực tác động lên vật:
\[mg.\left( {3\cos {\alpha _2} - 2\cos {\alpha _0}} \right) = mg\]
\[ \Leftrightarrow 3\cos {\alpha _2} - 2\cos {\alpha _0} = 1 \Leftrightarrow \cos {\alpha _2} = \frac{1}{3} + \frac{2}{3}.\cos {\alpha _0}\]
+ Suy ra: \[\frac{{{v_1}}}{{{v_2}}} = \frac{{\sqrt {2gl\left( {\cos {\alpha _1} - \cos {\alpha _0}} \right)} }}{{\sqrt {2gl\left( {\cos {\alpha _2} - \cos {\alpha _0}} \right)} }} = \sqrt {\frac{{\cos {\alpha _1} - \cos {\alpha _0}}}{{\cos {\alpha _2} - \cos {\alpha _0}}}} \]
\[ = \sqrt {\frac{{\frac{1}{2} + \frac{1}{2}.\cos {\alpha _0} - \cos {\alpha _0}}}{{\frac{1}{3} + \frac{2}{3}.\cos {\alpha _0} - \cos {\alpha _0}}}} = \sqrt {\frac{{\frac{1}{2}\left( {1 - \cos {\alpha _0}} \right)}}{{\frac{1}{3}\left( {1 - \cos {\alpha _0}} \right)}}} = \sqrt {\frac{3}{2}} \].
Câu 125:
Một sóng âm thanh được phát hiện bởi một micrô. Đầu ra từ micrô được kết nối với đầu vào Y của máy hiện sóng tia âm cực (CRO). Dấu vết trên CRO được hiển thị trên hình. Cài đặt cơ sở thời gian trên CRO là \[0,20ms\]mỗi lần chia Tần số của sóng âm là bao nhiêu?
Đáp án B
Phương pháp giải:
+ Công thức liên hệ giữa tần số và chu kì: \[f = \frac{1}{T}\].
+ Sử dụng kĩ năng đọc đồ thị.
Giải chi tiết:
Từ đồ thị ta thấy chu kì sóng âm là:
\[T = 4.0,20 = 0,8ms = {8.10^{ - 4}}s\]
\[ \Rightarrow \] Tần số của âm do âm thoa tạo ra là:
\[f = \frac{1}{T} = \frac{1}{{{{8.10}^{ - 4}}}} = 1250Hz\].
Câu 126:
Một nhà vật lý hạt nhân làm thí nghiệm xác định chu kỳ bán rã \(\left( T \right)\) của một chất phóng xạ bằng cách dùng máy đếm xung để đo tỉ lệ giữa số hạt bị phân rã \(\left( {\Delta N} \right)\) và số hạt ban đầu \(\left( {{N_0}} \right)\). Dựa vào kết quả thực nghiệm đo được trên hình vẽ, hãy tính \(T\)?
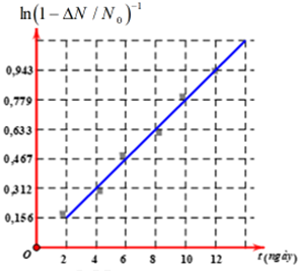
Đáp án D
Phương pháp giải:
Số hạt nhân bị phân rã: \(\Delta N = {N_0}\left( {1 - {2^{ - \frac{t}{T}}}} \right)\)
Giải chi tiết:
Ta có: \({\left( {1 - \frac{{\Delta N}}{{{N_0}}}} \right)^{ - 1}} = \frac{1}{{1 - \frac{{\Delta N}}{{{N_0}}}}} = \frac{1}{{1 - \left( {1 - {2^{ - \frac{t}{T}}}} \right)}} = \frac{1}{{{2^{ - \frac{t}{T}}}}} = {2^{\frac{t}{T}}}\)
\( \Rightarrow \ln {\left( {1 - \frac{{\Delta N}}{{{N_0}}}} \right)^{ - 1}} = \ln \left( {{2^{\frac{t}{T}}}} \right)\)
Từ đồ thị ta thấy:
\(\left\{ {\begin{array}{*{20}{l}}{t = 6ngay}\\{\ln {{\left( {1 - \frac{{\Delta N}}{{{N_0}}}} \right)}^{ - 1}} = 0,467}\end{array}} \right. \Rightarrow \ln \left( {{2^{\frac{6}{T}}}} \right) = 0,467 \Rightarrow T = 8,9ngay\).
Câu 127:
Một máy phát sóng điện từ đặt cách mặt phản xạ \(45cm\). Các sóng phát ra có tần số \(1,00GHz\). Một sóng dừng được tạo ra với một nút tại máy phát và một nút ở bề mặt. Có bao nhiêu bụng sóng trong không gian giữa máy phát và mặt phản xạ?
Đáp án A
Phương pháp giải:
Điều kiện có sóng dừng hai đầu cố định: \(l = \frac{{k\lambda }}{2} = \frac{{k.v}}{{2f}}\).
Trong đó: Số bụng = k; Số nút = k + 1.
Giải chi tiết:
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{l = 45cm = 0,45m}\\{v = c = {{3.10}^8}m/s}\\{f = 1GHz = {{10}^9}Hz}\end{array}} \right.\)
Một sóng dừng được tạo ra với một nút tại máy phát và một nút ở bề mặt.
Áp dụng điều kiện có sóng dừng với hai đầu là nút sóng ta có:
\(l = \frac{{k\lambda }}{2} = \frac{{k.v}}{{2f}} \Rightarrow k = \frac{{2.l.f}}{v} = \frac{{2.0,{{45.10}^9}}}{{{{3.10}^8}}} = 3\)
\( \Rightarrow \) Có 3 bụng sóng trong không gian giữa máy phát và mặt phản xạ.
Câu 128:
Một học sinh làm thí nghiệm đo bước sóng ánh sáng bằng thí nghiệm khe Y-âng. Trong khi tiến hành, học sinh này đo được khoảng cách hai khe sáng là \(1,00 \pm 0,05\left( {mm} \right)\); khoảng cách từ mặt phẳng chứa hai khe đến màn đo được là \(2000 \pm 1,54\left( {mm} \right)\); khoảng cách 10 vân sáng liên tiếp đo được là \(10,80 \pm 0,14\left( {mm} \right)\). Sai số tuyệt đối của quá trình đo bước sóng là
Đáp án B
Phương pháp giải:
Khoảng cách của 10 vân sáng liên tiếp: \(l = 9i\)
Bước sóng: \(\lambda = \frac{{ai}}{D}\)
Sai số tỉ đối: \(\frac{{\Delta \lambda }}{{\bar \lambda }} = \frac{{\Delta a}}{{\bar a}} + \frac{{\Delta i}}{{\bar i}} + \frac{{\Delta D}}{{\bar D}}\)
Sai số tuyệt đối: \(\Delta \lambda = \bar \lambda \left( {\frac{{\Delta a}}{{\bar a}} + \frac{{\Delta i}}{{\bar i}} + \frac{{\Delta D}}{{\bar D}}} \right)\)
Giải chi tiết:
Khoảng cách giữa 10 vân sáng liên tiếp là:
\(l = 9i \Rightarrow \left\{ {\begin{array}{*{20}{l}}{\bar i = \frac{{\bar l}}{9} = 1,2{\mkern 1mu} {\mkern 1mu} \left( {mm} \right)}\\{\Delta i = \frac{{\Delta l}}{9} = 0,016{\mkern 1mu} {\mkern 1mu} \left( {mm} \right)}\end{array}} \right.\)
Giá trị trung bình của bước sóng là:
\(\bar \lambda = \frac{{\bar a.\bar i}}{{\bar D}} = \frac{{{{1.10}^{ - 3}}.1,{{2.10}^{ - 3}}}}{2} = 0,{6.10^{ - 6}}{\mkern 1mu} {\mkern 1mu} \left( m \right) = 0,6{\mkern 1mu} {\mkern 1mu} \left( {\mu m} \right)\)
Sai số tỉ đối của phép đo là: \(\frac{{\Delta \lambda }}{{\bar \lambda }} = \frac{{\Delta a}}{{\bar a}} + \frac{{\Delta i}}{{\bar i}} + \frac{{\Delta D}}{{\bar D}}\)
\( \Rightarrow \frac{{\Delta \lambda }}{{0,6}} = \frac{{0,05}}{1} + \frac{{0,016}}{{1,2}} + \frac{{1,54}}{{2000}}\)
\( \Rightarrow \Delta \lambda \approx \pm 0,038{\mkern 1mu} {\mkern 1mu} \left( {\mu m} \right)\).
Câu 129:
Vật liệu chính được sử dụng trong một pin quang điện là
Đáp án D
Phương pháp giải:
Pin quang điện là nguồn điện trong đó quang năng chuyển hóa thành điện năng. Pin quang điện hoạt động dựa trên hiện tượng quang điện trong của các chất bán dẫn: german, silic, selen...
Giải chi tiết:
Vật liệu chính sử dụng trong một pin quang điện là bán dẫn.
Câu 130:
Đặt điện áp \(u = {U_0}\cos \omega t\) vào hai đầu đoạn mạch AB như hình bên. Trong đó, cuộn cảm thuần có độ tự cảm L; tụ điện có điện dung C; X là đoạn mạch chứa các phần tử có \({R_1},{L_1},{C_1}\) mắc nối tiếp. Biết \(2{\omega ^2}LC = 1\), các điện áp hiệu dụng: \({U_{AN}} = 120V;{U_{MB}} = 90V\), góc lệch pha giữa \({u_{AN}}\) và \({u_{MB}}\) là \(\frac{{5\pi }}{{12}}\). Hệ số công suất của X là
Đáp án: 0.868
Phương pháp giải:
+ Hệ số công suất của đoạn mạch X: \(\cos {\varphi _X}\)
Trong đó: \({\varphi _X} = {\varphi _{uX}} - {\varphi _i}\)
+ Pha ban đầu của i: \({\varphi _i} = {\varphi _{uC}} + \frac{\pi }{2} = {\varphi _{uL}} - \frac{\pi }{2}\)
Giải chi tiết:
Ta có: \(2LC{\omega ^2} = 1 \Leftrightarrow \frac{{2\omega L}}{{\frac{1}{{\omega C}}}} = 1 \Rightarrow 2{Z_L} = {Z_C}\)
\( \Rightarrow 2{u_L} = - {u_C} \Rightarrow 2{u_L} + {u_C} = 0\)
\( \Rightarrow 2{u_{AN}} + {u_{MB}} = 2{u_L} + 2{u_X} + {u_X} + {u_C}\)
\( \Rightarrow 2{u_{AN}} + {u_{MB}} = 3{u_X}\)
\( \Rightarrow {u_X} = \frac{{2{u_{AN}} + {u_{MB}}}}{3}\)
Giả sử \({\varphi _{uMB}} = 0 \Rightarrow {\varphi _{uAN}} = \frac{{5\pi }}{{12}}\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{u_{MB}} = 90\sqrt 2 \cos \left( {\omega t} \right)}\\{{u_{AN}} = 120\sqrt 2 .\cos \left( {\omega t + \frac{{5\pi }}{{12}}} \right)}\end{array}} \right.\)
\( \Rightarrow {u_X} = \frac{{240\sqrt 2 \angle \frac{{5\pi }}{{12}} + 90\sqrt 2 \angle 0}}{3} = 130,7\angle 0,99\)
\( \Rightarrow {\varphi _{uX}} = 0,99rad\)
Lại có: \({u_C} = {u_{MB}} - {u_X} = 122,6\angle - 1,1\)
\( \Rightarrow {\varphi _i} = {\varphi _{uC}} + \frac{\pi }{2} = - 1,1 + \frac{\pi }{2} \approx 0,47079rad\)
\( \Rightarrow \) Độ lệch pha giữa \({u_X}\) và \(i\) là:
\({\varphi _X} = {\varphi _{uX}} - {\varphi _i} = 0,99 - 0,47079 = 0,51921rad\)
\( \Rightarrow \) Hệ số công suất của X là: \(\cos {\varphi _X} = \cos 0,51921 = 0,868\).
Câu 131:
Cho hỗn hợp chất rắn gồm CaC2, Al4C3, Ca vào nước dư thu được hỗn hợp X gồm 3 khí (trong đó có 2 khí có cùng số mol). Lấy 8,96 lít hỗn hợp X (đktc) chia làm 2 phần bằng nhau. Phần 1 cho vào dung dịch AgNO3 trong NH3 (dư), sau phản ứng thu được 24 gam kết tủa. Phần 2 cho qua Ni (đun nóng) thu được hỗn hợp Y. Thể tích O2 (đktc) cần dùng để đốt cháy hoàn toàn Y là
Đáp án D
Phương pháp giải:
CaC2, Al4C3, Ca tác dụng với H2O thu được hỗn hợp X gồm 3 khí lần lượt là C2H2; CH4 và H2.
Phần 1: Chỉ có C2H2 pư
PTHH: C2H2 + AgNO3 + NH3 → Ag2C2↓ + NH4NO3
Từ số mol kết tủa Ag2C2 suy ra số mol C2H2.
Hỗn hợp X có 2 khí có số mol bằng nhau ⟹ nCH4 = nH2.
Phần 2: Thành phần nguyên tố của hỗn hợp X và Y giống nhau nên đốt Y cũng như đốt X.
\(\left\{ {\begin{array}{*{20}{l}}{{C_2}{H_2}}\\{C{H_4}}\\{{H_2}}\end{array}} \right. + {O_2} \to \left\{ {\begin{array}{*{20}{l}}{C{O_2}}\\{{H_2}O}\end{array}} \right.\)
BTNT.C ⟹ nCO2 = 2nC2H2 + nCH4
BTNT.H ⟹ nH2O = nC2H2 + 2nCH4 + nH2
BTNT.O ⟹ nO2 pư = nCO2 + ½ nH2O ⟹ VO2 (đktc).
Giải chi tiết:
CaC2, Al4C3, Ca tác dụng với H2O thu được hỗn hợp X gồm 3 khí lần lượt là C2H2; CH4 và H2.
nX = 8,96/22,4 = 0,4 (mol) ⟹ nX trong mỗi phần = 0,2 (mol)
Phần 1: Chỉ có C2H2 pư
PTHH: C2H2 + AgNO3 + NH3 → Ag2C2↓ + NH4NO3
⟹ nC2H2 = nAg2C2 = 24/240 = 0,1 (mol)
⟹ (nCH4 + nH2) = nX - nC2H2 = 0,2 - 0,1 = 0,1 (mol)
Hỗn hợp X có 2 khí có số mol bằng nhau ⟹ nCH4 = nH2 = 0,1/2 = 0,05 (mol) (vì nếu C2H2 bằng với mol 1 chất khí còn lại thì vô lí).
Phần 2: Thành phần nguyên tố của hỗn hợp X và Y giống nhau nên đốt Y cũng như đốt X.
\(\left\{ {\begin{array}{*{20}{l}}{{C_2}{H_2}:0,1}\\{C{H_4}:0,05}\\{{H_2}:0,05}\end{array}} \right. + {O_2} \to \left\{ {\begin{array}{*{20}{l}}{C{O_2}:0,25\left( {BTNT.C} \right)}\\{{H_2}O:0,25\left( {BTNT.H} \right)}\end{array}} \right.\)
BTNT.O ⟹ nO2 pư = nCO2 + ½ nH2O = 0,25 + ½.0,25 = 0,375 mol
⟹ VO2 (đktc) = 0,375.22,4 = 8,4 (lít).
Câu 132:
Pha chế 35,8 gam dung dịch CuSO4 bão hòa ở 100oC. Đun nóng dung dịch này cho đến khi có 17,86 gam nước bay hơi, sau đó để nguội đến 20oC. Tính số gam tinh thể CuSO4.5H2O kết tinh. Biết rằng độ tan của CuSO4 trong nước ở 20oC và 100oC lần lượt là 20,26 gam và 75,4 gam.
Đáp án A
Phương pháp giải:
Độ tan (S) của một chất trong nước là số gam chất đó hòa tan trong 100 gam nước để tạo thành dung dịch bão hòa ở một nhiệt độ xác định.
Giải chi tiết:
*Ở 100oC, độ tan của CuSO4 là 75,4 gam
Tức trong 175,4 gam dung dịch bão hòa có 75,4 gam CuSO4 và 100 gam H2O
⟹ 35,8 gam ⟶ 15,4 gam CuSO4
Gọi x là số mol CuSO4.5H2O kết tinh
*Ở 20oC, độ tan của CuSO4 là 20,26 gam
Tức trong 120,26 gam dung dịch bão hòa có 20,26 gam CuSO4 và 100 gam H2O
Theo đề: (35,8 - 17,86 - 250x) gam (15,4 - 160x) gam
⟹ 120,26.(15,4 - 160x) = 20,26.(35,8 - 17,86 - 250x)
⟹ x = 0,105
⟹ mCuSO4.5H2O = 0,105.250 = 26,25 gam.Câu 133:
Nung 0,935 gam quặng cromit với chất oxi hóa để oxi hóa toàn bộ crom thành CrO42-. Hòa tan sản phẩm vào nước, phân hủy hết chất oxi hóa, axit hóa dung dịch bằng H2SO4 rồi thêm 50,0 ml dung dịch FeSO4 0,08M vào. Để chuẩn độ FeSO4 dư cần 14,85 ml dung dịch KMnO4 0,004M. Hàm lượng crom có trong quặng là
Đáp án B
Phương pháp giải:
Tính theo các phương trình ion thu gọn:
3Fe2+ + CrO42- + 8H+ ⟶ 3Fe3+ + Cr3+ + 4H2O (1)
5Fe2+ + MnO4- + 8H+ ⟶ 5Fe3+ + Mn2+ + 4H2O (2)
Giải chi tiết:
\({n_{F{{\rm{e}}^{2 + }}\left( {b{\rm{d}}} \right)}} = 0,05.0,08 = 0,004\left( {mol} \right)\)
\({n_{KMn{O_4}}} = 0,01485.0,004 = 5,{94.10^{ - 5}}\left( {mol} \right)\)
3Fe2+ + CrO42- + 8H+ ⟶ 3Fe3+ + Cr3+ + 4H2O (1)
5Fe2+ + MnO4- + 8H+ ⟶ 5Fe3+ + Mn2+ + 4H2O (2)
Theo (2) ⟹ nFe2+(dư) = 5.nMnO4- = 5.5,94.10-5 = 2,97.10-4 (mol)
⟹ nFe2+(pư) = 0,004 - 2,97.10-4 = 3,703.10-3 (mol)
Theo (1) ⟹ nCrO42- = 1/3.nFe2+(pư) = 1/3.3,703.10-3 = 1,23433.10-3 (mol)
⟹ mCr = 1,23433.10-3.52 = 0,064 gam.
⟹ %mCr = \(\frac{{0,064}}{{0,935}}.100\% \)= 6,845%.
Câu 134:
Cho a gam hỗn hợp X gồm glyxin, alanin và valin phản ứng với 100 ml dung dịch HCl 1M thu được dung dịch Y. Để phản ứng hết với các chất trong dung dịch Y cần 380 ml dung dịch KOH 0,5M. Mặt khác, đốt cháy hoàn toàn a gam hỗn hợp X rồi cho sản phẩm cháy vào bình đựng dung dịch Ba(OH)2 dư, sau phản ứng khối lượng dung dịch trong bình giảm 43,74 gam. Giá trị của a là
Đáp án B
Phương pháp giải:
- Để đơn giản hóa, coi dung dịch Y gồm các amino axit và HCl
⟹ nKOH = nHCl + nCOOH
⟹ nCOOH = nKOH - nHCl
- Công thức chung của hỗn hợp X là: CnH2n+1NO2
CnH2n+1NO2 (X) + O2 nCO2 + \[\frac{{2n + 1}}{2}\] H2O + ½ N2
Từ PT phản ứng cháy ⟹ nX = (nH2O - nCO2)/0,5
- Đặt nCO2 = x mol; nH2O = y mol
Lập hệ PT tìm x, y dựa vào:
+) Quan hệ với nX.
+) Khối lượng dung dịch Ba(OH)2 giảm.
- Tính số mol các nguyên tố trong X ⟹ a.
Giải chi tiết:
- Để đơn giản hóa, coi dung dịch Y gồm các amino axit và HCl
⟹ nKOH = nHCl + nCOOH
⟹ nCOOH = nKOH - nHCl = 0,38.0,5 - 0,1.1 = 0,09 mol.
Các chất trong X chứa 1 nhóm COOH ⟹ nX = nCOOH = 0,09 mol
- Công thức chung của hỗn hợp X là: CnH2n+1NO2
CnH2n+1NO2 (X) + O2 nCO2 + \[\frac{{2n + 1}}{2}\] H2O + ½ N2
Từ PT phản ứng cháy ⟹ nX = (nH2O - nCO2)/0,5
Đặt nCO2 = x mol; nH2O = y mol
⟹ (y - x)/0,5 = 0,09 ⟹ y - x = 0,045 (1)
- Cho sản phẩm cháy vào bình đựng Ba(OH)2 dư:
CO2 + Ba(OH)2 → BaCO3 ↓ + H2O
x → x (mol)
mdd giảm = m ↓ - mCO2 - mH2O = 43,74 g.
⟹ 197x - 44x - 18y = 43,74
⟹ 153x - 18y = 43,74 (2)
Từ (1)(2) ⟹ x = 0,33; y = 0,375
⟹ nC = nCO2 = 0,33 mol
nH = 2nH2O = 2.0,375 = 0,75 mol
nO = 2nCOOH = 2.0,09 = 0,18 mol
nN = nX = 2.0,045 = 0,09 mol
⟹ a = 0,33.12 + 0,75 + 0,18.16 + 0,09.14 = 8,85 gam.
Câu 135:
Tiến hành thí nghiệm theo các bước sau:
Bước 1: Cho vào hai bình cầu mỗi bình khoảng 6 ml metyl axetat.
Bước 2: Thêm khoảng 6 - 8 ml dung dịch H2SO4 loãng 25% vào bình thứ nhất, khoảng 12 ml dung dịch NaOH 35% vào bình thứ hai.
Bước 3: Lắc đều cả hai bình, lắp ống sinh hàn rồi đun sôi nhẹ trong khoảng thời gian 5 - 8 phút, sau đó để nguội.
Phát biểu nào sau đây đúng?
Đáp án B
Phương pháp giải:
Dựa vào lý thuyết về phản ứng thủy phân este.
Giải chi tiết:
A sai, vì phản ứng thủy phân este trong MT axit không được gọi là phản ứng xà phòng hóa.
B đúng.
C sai, phản ứng thủy phân este trong MT axit là thuận nghịch nên luôn còn 1 lượng este dư do đó bình 1 không đồng nhất.
D sai, vai trò của ống sinh hàn là ngưng tụ este tránh thất thoát sản phẩm.
Câu 136:
Polime nào sau đây có chứa nguyên tố nitơ?
Đáp án D
Phương pháp giải:
Dựa vào lý thuyết về polime.
Giải chi tiết:
A: Polibutadien (-CH2-CH=CH-CH2-)n → chứa C, H.
B: Poli(vinyl clorua) (-CH2-CHCl-)n → chứa C, H, Cl.
C: Xenlulozơ (C6H10O5)n → chứa C, H, O.
D: Protein → chứa C, H, O, N.
Câu 137:
Nhiệt phân hoàn toàn m gam hỗn hợp Al(NO3)3 và Fe(NO3)2 thu được 47,3 gam chất rắn Y. Hòa tan Y trong dung dịch NaOH thấy có 0,3 mol NaOH phản ứng. Khối lượng hỗn hợp muối là
Đáp án B
Phương pháp giải:
Viết PTHH phản ứng nhiệt phân muối nitrat ⟹ Chất rắn Y gồm Fe2O3 và Al2O3.
Khi cho Y vào NaOH thì chỉ có Al2O3 phản ứng; từ mol NaOH ⟹ số mol Al2O3.
Từ khối lượng chất rắn Y ⟹ khối lượng Fe2O3 ⟹ số mol Fe2O3.
Sử dụng bảo toàn nguyên tố Fe, Al để tính số mol Fe(NO3)2, Al(NO3)3 trong hỗn hợp ban đầu.
Tính giá trị của m.
Giải chi tiết:
2Fe(NO3)2 → Fe2O3 + 4NO2 + 0,5O2
4Al(NO3)3 → 2Al2O3 + 12NO2 + 3O2
⟹ Chất rắn Y gồm Fe2O3 và Al2O3
Khi cho Y vào NaOH thì chỉ có Al2O3 phản ứng
2NaOH + Al2O3 → 2NaAlO2 + H2O.
0,3 → 0,15
⟹ mAl2O3 = 102.0,15 = 15,3 gam
⟹ mFe2O3 = mchất rắn - mAl2O3 = 47,3 - 15,3 = 32 gam
⟹ nFe2O3 = 0,2 mol
Bảo toàn nguyên tố Fe ⟹ nFe(NO3)2 = 2nFe2O3 = 0,4 mol ⟹ mFe(NO3)2 = 72 gam
Bảo toàn nguyên tố Al ⟹ nAl(NO3)3 = 2nAl2O3 = 0,3 mol ⟹ mAl(NO3)3 = 63,9 gam
⟹ m = mFe(NO3)2 + mAl(NO3)3 = 135,9 gam.
Câu 138:
Tiến hành thí nghiệm như hình vẽ:
Ban đầu trong cốc chứa nước vôi trong. Sục rất từ từ CO2 vào cốc cho tới dư. Hỏi độ sáng của bóng đèn thay đổi như thế nào?
Đáp án A
Giải chi tiết:
+ Khi CO2 vào thì ban đầu nước vôi trong dư so với CO2 nên ion Ca2+ dần đến hết vì bị kết tủa thành CaCO3
⟹ lượng ion trong dung dịch giảm dần về 0
+ Khi CO2 dư thì kết tủa lại bị hòa tan, tạo thành ion Ca2+ và HCO3-
⟹ lượng ion tăng dần
Vậy đèn có độ sáng giảm dần đến tắt rồi lại sáng tăng dần.
Câu 139:
Đáp án C
Phương pháp giải:
Nguyên lí chuyển dịch cân bằng Lơ Sa-tơ-li-ê: Một phản ứng thuận nghịch đang ở trạng thái cân bằng khi chịu một tác động từ bên ngoài như biến đổi nồng độ, áp suất, nhiệt độ, thì cân bằng sẽ chuyển dịch theo chiều làm giảm tác động bên ngoài đó.
Giải chi tiết:
A. Tăng lượng H2O ⟹ CB chuyển dịch theo chiều làm giảm H2O ⟹ chiều thuận.
B. Thêm H2 ⟹ CB chuyển dịch theo chiều làm giảm H2 ⟹ chiều nghịch.
C. Dùng xúc tác ⟹ tăng tốc độ cả phản ứng thuận và nghịch ⟹ không làm chuyển dịch cân bằng.
D. Tăng nhiệt độ ⟹ CB chuyển dịch theo chiều giảm nhiệt độ tức là chiều thu nhiệt ⟹ chiều thuận.
Câu 140:
Este X hai chức, mạch hở, tạo bởi một ancol no với hai axit cacboxylic no, đơn chức. Este Y ba chức, mạch hở tạo bởi glixerol với một axit cacboxylic không no, đơn chức (phân tử có hai liên kết π). Đốt cháy hoàn toàn m gam hỗn hợp E gồm X và Y cần vừa đủ 0,5 mol O2 thu được 0,45 mol CO2. Mặt khác, thủy phân hoàn toàn 0,16 mol E cần vừa đủ 210 ml dung dịch NaOH 2M thu được hai ancol (có cùng số nguyên tử cacbon trong phân tử) và hỗn hợp ba muối, trong đó tổng khối lượng hai muối của hai axit no là a gam. Giá trị của a là
Đáp án: 12,36
Phương pháp giải:
- Xét trong 0,16 mol hỗn hợp E:
Từ số mol hỗn hợp và số mol NaOH ⟹ nX, nY ⟹ tỉ lệ nX : nY.
- Xét m gam hỗn hợp E:
Quy đổi hỗn hợp E thành (HCOO)2C3H6 (a mol); (CH2=CHCOO)3C3H5 (b mol); CH2 (c mol)
Đốt cháy E:
(HCOO)2C3H6 + 5O2 → 5CO2 + 4H2O
(CH2=CHCOO)3C3H5 + 12,5O2 → 12CO2 + 7H2O
CH2 + 1,5O2 → CO2 + H2O
Từ số mol O2 ⟹ phương trình (*)
Từ số mol CO2 ⟹ phương trình (**)
Từ tỉ lệ nX : nY ⟹ phương trình (***)
Giải hệ tìm được a, b, c.
Gọi số nhóm CH2 cần trả cho X, Y lần lượt là m và n (n phải chẵn do Y tạo bởi 1 axit).
Lập phương trình mối liên hệ giữa m và n. Biện luận tìm giá trị m, n thỏa mãn.
Từ đó tính được khối lượng muối của axit cacboxylic no.
Lưu ý: Lượng chất ở 2 thí nghiệm khác nhau.
Giải chi tiết:
- Xét trong 0,16 mol hỗn hợp E:
+) nhh E = nX + nY = 0,16 (1)
+) nNaOH = 2nX + 3nY = 0,42 (2)
⟹ nX = 0,06 và nY = 0,1 (mol)
⟹ nX : nY = 3 : 5.
- Xét m gam hỗn hợp E:
Quy đổi hỗn hợp E thành (HCOO)2C3H6 (a mol); (CH2=CHCOO)3C3H5 (b mol); CH2 (c mol)
Đốt cháy E:
(HCOO)2C3H6 + 5O2 → 5CO2 + 4H2O
a → 5a → 5a
(CH2=CHCOO)3C3H5 + 12,5O2 → 12CO2 + 7H2O
b → 12,5b → 12b
CH2 + 1,5O2 → CO2 + H2O
c → 1,5c → c
⟹ nO2 = 5a + 12,5b + 1,5c = 0,5 (*)
⟹ nCO2 = 5a + 12b + c = 0,45 (**)
Mà nX : nY = 3 : 5 ⟹ 5a - 3b = 0 (***)
Từ (*) (**) (***) ⟹ a = 0,015; b = 0,025; c = 0,075.
Gọi số nhóm CH2 cần trả cho X, Y lần lượt là m và n (n phải chẵn do Y tạo bởi 1 axit).
⟹ 0,015m + 0,025n = 0,075 ⟹ 3m + 5n = 15
+ Nếu n = 0 ⟹ m = 5 (thỏa mãn) ⟹ không cần trả CH2 cho Y.
+ Nếu n = 2 ⟹ m = 1,67 (loại).
Muối của axit no gồm: HCOONa (0,03) và CH2 (0,075)
⟹ mmuối = 3,09 gam.
Như vậy tỉ lệ:
0,04 mol E tạo 3,09 gam muối của axit cacboxylic no.
⟹ 0,16 mol …….. 12,36 gam.
Câu 141:
Phát biểu nào sau đây là đúng khi nói về áp suất rễ
Đáp án B
Giải chi tiết:
Áp suất rễ là lực đẩy nước của rễ lên thân là động lực của dòng mạch gỗ.
Câu 142:
Đáp án A
Giải chi tiết:
Chiều hướng tiến hóa về tổ chức thần kinh ở động vật theo trình tự là hệ thần kinh dạng lưới → hệ thần kinh dạng chuỗi hạch → hệ thần kinh dạng ống.
Câu 143:
Trong sản xuất nông nghiệp, khi sử dụng các chất kích thích sinh trưởng nhân tạo, cần phải chú ý nguyên tắc quan trọng nhất để đảm bảo an toàn cho sản phẩm thu hoạch là
Đáp án A
Giải chi tiết:
Khi sử dụng các chất kích thích sinh trưởng nhân tạo cần chú ý sử dụng với nồng độ tối thích, không sử dụng trên nông phẩm trực tiếp làm thức ăn.
Câu 144:
Các hình thức sinh sản vô tính ở thực vật đều dựa trên cơ sở của quá trình
Đáp án C
Giải chi tiết:
Các hình thức sinh sản vô tính ở thực vật đều dựa trên cơ sở của quá trình nguyên phân, tạo ra các tế bào giống với tế bào ban đầu.
Câu 145:
Đáp án B
Phương pháp giải:
Thể một có dạng: 2n – 1
Kì sau nguyên phân: Các cromatit tách nhau ra thành các NST đơn và di chuyển về 2 cực.
Giải chi tiết:
2n = 28 → thể một: 2n – 1 = 27.
Trong kì giữa của nguyên phân, trong mỗi tế bào có 27 NST kép (mỗi NST kép có 2 cromatit)
Kì sau nguyên phân: Các cromatit tách nhau ra thành các NST đơn và di chuyển về 2 cực, trong mỗi tế bào có 27 × 2 = 54 NST đơn.
Câu 146:
Xét gen A có 2 alen là A và a. Một quần thể đang cân bằng di truyền có tần số A = 0,6 thì kiểu gen Aa chiếm tỉ lệ
Đáp án D
Phương pháp giải:
Bước 1: tính tần số alen a
Bước 2: tính tỉ lệ Aa
Quần thể cân bằng di truyền có cấu trúc p2AA + 2pqAa +q2aa =1
Giải chi tiết:
Tần số alen a = 1 – 0,6A =0,4
Tỉ lệ kiểu gen Aa = 2 × 0,6 × 0,4 = 0,48.
Câu 147:
Hiện tượng con lai hơn hẳn bố mẹ về sinh trưởng, phát triển, năng suất và sức chống chịu được gọi là gì?
Đáp án C
Giải chi tiết:
Hiện tượng con lai hơn hẳn bố mẹ về sinh trưởng, phát triển, năng suất và sức chống chịu được gọi là ưu thế lai (SGK Sinh 12 trang 77).
Câu 148:
Theo Đacuyn, nguyên liệu chủ yếu cho chọn lọc tự nhiên là
Đáp án C
Giải chi tiết:
Theo Đacuyn, nguyên liệu chủ yếu cho chọn lọc tự nhiên là biến dị cá thể, ông chưa biết tới các khái niệm còn lại.
Câu 149:
Hiện tượng liền rễ ở cây thông nhựa là ví dụ minh họa cho mối quan hệ
Đáp án A
Giải chi tiết:
Hiện tượng liền rễ ở cây thông nhựa là ví dụ minh họa cho mối quan hệ hỗ trợ cùng loài.
Câu 150:
Cho biết mỗi gen quy định một tính trạng, các gen phân li độc lập, gen trội là trội hoàn toàn và không có đột biến xảy ra. Tính theo lý thuyết, phép lai AaBbDdEe × AaBbDdEe cho đời con có kiểu hình mang 2 tính trạng trội và 2 tính trạng lặn chiếm tỉ lệ
Đáp án: \[\frac{{27}}{{128}}\]
Trong trường hợp: 1 gen quy định 1 tính trạng, trội là trội hoàn toàn.
Xét 1 cặp gen: Aa × Aa → 1AA:2Aa:1aa → 3/4 trội: 1/4 lặn.
Giả sử có n cặp gen, tính kiểu hình trội về a tính trạng: \[C_n^a \times {\left( {\frac{3}{4}} \right)^a} \times {\left( {\frac{1}{4}} \right)^{n - a}}\]
Giải chi tiết:
Phép lai: AaBbDdEe × AaBbDdEe
Xét 1 cặp gen: Aa × Aa → 1AA:2Aa:1aa → 3/4 trội: 1/4 lặn, tương tự với các cặp gen khác.
Giả sử có 4 cặp gen, tính kiểu hình trội về 2 tính trạng: \[C_4^2 \times {\left( {\frac{3}{4}} \right)^2} \times {\left( {\frac{1}{4}} \right)^2} = \frac{{27}}{{128}}\].
