Cho hàm số \[f\left( x \right) = {2^x}{.7^{{x^2}}}\]. Khẳng định nào sau đây là khẳng định sai?
A.\[f\left( x \right) < 1 \Leftrightarrow x + {x^2}{\log _2}7 < 0\]
B. \[f\left( x \right) < 1 \Leftrightarrow x\ln 2 + {x^2}\ln 7 < 0\]
C. \[f\left( x \right) < 1 \Leftrightarrow x{\log _7}2 + {x^2} < 0\]
D. \[f\left( x \right) < 1 \Leftrightarrow 1 + x{\log _2}7 < 0\]
Giải bởi qa.haylamdo.com
\[\begin{array}{l}f\left( x \right) < 1 \Leftrightarrow {2^x}{.7^{{x^2}}} < 1\\ \Leftrightarrow {7^{{x^2}}} < {2^{ - x}}\\ \Leftrightarrow {x^2}.\ln 7 < - x.\ln 2\\ \Leftrightarrow x\ln 2 + {x^2}\ln 7 < 0\\ \Leftrightarrow x + {x^2}{\log _2}7 < 0\\ \Leftrightarrow x{\log _7}2 + {x^2}\end{array}\]
Đối chiếu các đáp án thấy câu D sai.
Đáp án cần chọn là: D
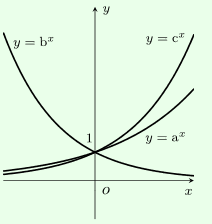
Cho các đồ thị hàm số \[y = {a^x},y = {b^x},y = {c^x}(0 < a,b,c \ne 1)\] chọn khẳng định đúng:
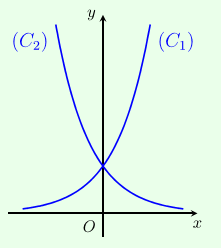
Cho hai hàm số \[y = {a^x},y = {b^x}\] với \[1 \ne a,b > 0\;\]lần lượt có đồ thị là (C1),(C2) như hình bên. Mệnh đề nào đúng?
Hàm số nào sau đây nghịch biến trên \[\left( { - \infty ; + \infty } \right)\]?
Tìm tất cả các giá trị thực của m để hàm số \[y = {2^{{x^3} - {x^2} + mx + 1}}\] đồng biến trên (1;2)
Tính đạo hàm của hàm số \[y = f\left( x \right) = {x^\pi }.{\pi ^x}\] tại điểm x=1.
