Chọn mệnh đề đúng:
A.lim
B. \mathop {\lim }\limits_{x \to 0} \frac{{\ln \left( {1 - x} \right)}}{x} = 1
C. \mathop {\lim }\limits_{x \to 0} \frac{{\ln x}}{x} = 1
D. \mathop {\lim }\limits_{x \to 0} \frac{{\ln \left( {1 + x} \right)}}{{1 + x}} = 1
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Giới hạn cần nhớ: \mathop {\lim }\limits_{x \to 0} \frac{{\ln \left( {1 + x} \right)}}{x} = 1
Đáp án cần chọn là: A
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = log\left( {{x^2} - 2mx + 4} \right)có tập xác định là R
Cho a,b là các số thực dương, thỏa mãn {a^{\frac{3}{4}}} > {a^{\frac{4}{5}}} và {\log _b}\frac{1}{2} < {\log _b}\frac{2}{3}. Mệnh đề nào dưới đây đúng?
Cho hai hàm số y = \ln \left| {\frac{{x - 2}}{x}} \right|vày = \frac{3}{{x - 2}} - \frac{1}{x} + 4m - 2020. Tổng tất cả các giá trị nguyên của tham số m để hai đồ thị hàm số cắt nhau tại một điểm duy nhất bằng:
Điểm nào sau đây không thuộc đồ thị hàm số y = lo{g_a}x(0 < a \ne 1)\;?
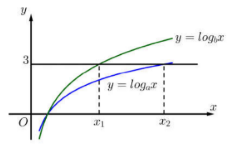
Hàm số y = {\log _a}xvà y = {\log _b}x có đồ thị như hình vẽ bên:
Đường thẳng y = 3 cắt hai đồ thị tại các điểm có hoành độ {x_1},{x_2}. Biết rằng {x_2} = 2{x_1},, giá trị của ab bằng:
Hàm số y = {\log _{\frac{e}{3}}}\left( {x - 1} \right) nghịch biến trên khoảng nào dưới đây?
Cho a,b là các số thực, thỏa mãn 0<a<1<b, khẳng định nào sau đây là đúng?
Tìm tham số m để hàm số y = \frac{{{{\log }_{\frac{1}{2}}}x - 2}}{{{{\log }_2}x - m}} đồng biến trên khoảng (0;1).
Tiệm cận đứng của đồ thị hàm số y = {\log _a}x(0 < a \ne 1) là đường thẳng:
Tập xác định của hàm số f\left( x \right) = {\log _{\frac{1}{2}}}\left( {{{\log }_4}\left( {{{\log }_{\frac{1}{4}}}\left( {{{\log }_{16}}\left( {{{\log }_{\frac{1}{{16}}}}x} \right)} \right)} \right)} \right) là một khoảng có độ dài n/m, với m và n là các số nguyên dương và nguyên tố cùng nhau. Khi đó m−n bằng:
Điểm ({x_0};{y_0})\;thuộc đồ thị hàm số y = lo{g_a}x(0 < a \ne 1)\; nếu:
Tìm tập giá trị T của hàm số f'\left( x \right) = \frac{{1 - \ln x}}{{{x^2}}} với x \in [1;{e^2}].