Tìm tham số m để tổng các nghiệm của phương trình sau đạt giá trị nhỏ nhất \[1 + \left[ {2{x^2} - m\left( {m + 1} \right)x - 2} \right]{.2^{1 + mx - {x^2}}} = \left( {{x^2} - mx - 1} \right){.2^{mx\left( {1 - m} \right)}} + {x^2} - {m^2}x\].
A.0
B.2
C.\( - \frac{1}{2}\)
D. \(\frac{1}{2}\)
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Ta có:
\[1 + \left[ {2{x^2} - m\left( {m + 1} \right)x - 2} \right]{.2^{1 + mx - {x^2}}} = \left( {{x^2} - mx - 1} \right){.2^{mx\left( {1 - m} \right)}} + {x^2} - {m^2}x\]
\[ \Leftrightarrow \left[ {\left( {{x^2} - {m^2}x - 1} \right) + \left( {{x^2} - mx - 1} \right)} \right]{.2^{ - \left( {{x^2} - mx - 1} \right)}} = \left( {{x^2} - mx - 1} \right){.2^{\left( {{x^2} - {m^2}x - 1} \right) - \left( {{x^2} - mx - 1} \right)}} + {x^2} - {m^2}x - 1\]
Đặt\(\left\{ {\begin{array}{*{20}{c}}{u = {x^2} - {m^2}x - 1}\\{v = {x^2} - mx - 1}\end{array}} \right.\) Phương trình trở thành:
\[\left( {u + v} \right){.2^{ - v}} = v{.2^{u - v}} + u \Leftrightarrow u\left( {{2^{ - v}} - 1} \right) = v{2^{ - v}}\left( {{2^u} - 1} \right)\left( * \right)\]
+) Dễ dàng kiểm tra u=0 hoặc v=0 là nghiệm của (*)
+) Với \[u,v \ne 0,\left( * \right) \Leftrightarrow \frac{{{2^{ - v}} - 1}}{{v{2^{ - v}}}} = \frac{{{2^u} - 1}}{u}\]
\[ \Leftrightarrow \frac{{{2^u} - 1}}{u} = \frac{{1 - {2^v}}}{v}\]
\[ \Leftrightarrow \frac{{{2^u} - 1}}{u} + \frac{{{2^v} - 1}}{v} = 0\]
Xét hàm\[f\left( t \right) = \frac{{{2^t} - 1}}{t}\] trên\[\mathbb{R} \setminus \left\{ 0 \right\}\] ta thấy:
+) Với t>0 thì\(\left\{ {\begin{array}{*{20}{c}}{{2^t} - 1 > 0}\\{t > 0}\end{array}} \right. \Rightarrow \frac{{{2^t} - 1}}{t} > 0 \Rightarrow f\left( t \right) > 0\)
+) Với t<0 thì \(\left\{ {\begin{array}{*{20}{c}}{{2^t} - 1 < 0}\\{t < 0}\end{array}} \right. \Rightarrow \frac{{{2^t} - 1}}{t} > 0 \Rightarrow f\left( t \right) > 0\)</0 thì>
Do đó \[f\left( t \right) > 0\] với mọi \[t \ne 0\]
\[ \Rightarrow f\left( u \right) > 0,f\left( v \right) > 0,\forall u,v \ne 0\]
\[ \Rightarrow f\left( u \right) + f\left( v \right) > 0,\forall u,v \ne 0\]
\[ \Rightarrow \frac{{{2^u} - 1}}{u} + \frac{{{2^v} - 1}}{v} > 0,\forall u,v \ne 0\]
Do đó phương trình\[\frac{{{2^u} - 1}}{u} + \frac{{{2^v} - 1}}{v} = 0\] vô nghiệm.
Vậy \(\left[ {\begin{array}{*{20}{c}}{u = 0}\\{v = 0}\end{array}} \right.\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{x^2} - {m^2}x - 1 = 0(1)}\\{{x^2} - mx - 1 = 0(2)}\end{array}} \right.\)
Hai phương trình trên luôn có hai nghiệm phân biệt, tổng hai nghiệm ở mỗi phương trình là:
\[{S_1} = {m^2},\,{S_2} = m \Rightarrow S = {m^2} + m \ge - \frac{1}{4}\]
Vậy tổng các nghiệm của phương trình đã cho nhỏ nhất là \[ - \frac{1}{4}\] khi \[m = - \frac{1}{2}\]Đáp án cần chọn là: C
Phương trình \[{2^{23{x^3}}}{.2^x} - {1024^{{x^2}}} + 23{x^3} = 10{x^2} - x\] có tổng các nghiệm gần nhất với số nào dưới đây:
Có bao nhiêu giá trị nguyên dương của tham số m để phương trình \[{16^x} - {2.12^x} + \left( {m - 2} \right){.9^x} = 0\]có nghiệm dương?
Cho hàm số y=f(x) có bảng biến thiên như sau
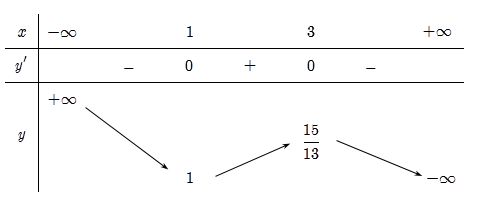
Biết f(0)=76, giá trị lớn nhất của mm để phương trình \[{e^{2{f^3}\left( x \right) - \frac{{13}}{2}{f^2}\left( x \right) + 7f\left( x \right) + \frac{3}{2}}} = m\] có nghiệm trên đoạn \[\left[ {0;2} \right]\;\]là
Tìm tập hợp tất cả các nghiệm của phương trình \[{2^{{x^2} + x - 1}} = \frac{1}{2}\].
Tìm nghiệm của phương trình \[\frac{{{3^{2x - 6}}}}{{27}} = {\left( {\frac{1}{3}} \right)^x}.\]
Biết phương trình \[{9^x} - {2^{x + \frac{1}{2}}} = {2^{x + \frac{3}{2}}} - {3^{2x - 1}}\]có nghiệm là a. Tính giá trị của biểu thức \[P = a + \frac{1}{2}lo{g_{\frac{9}{2}}}2\;\].
Tìm nghiệm của phương trình \[{9^{\sqrt {x - 1} }} = {e^{\ln 81}}\]
Tìm giá trị của a để phương trình \[{(2 + \sqrt 3 )^x} + (1 - a){(2 - \sqrt 3 )^x} - 4 = 0\;\]có 2 nghiệm phân biệt thỏa mãn:\[{x_1} - {x_2} = lo{g_{2 + \sqrt 3 }}3\], ta có a thuộc khoảng:
Phương trình \[x({2^{x - 1}} + 4) = {2^{x + 1}} + {x^2}\]có tổng các nghiệm bằng
Tìm m để phương trình \[{4^x} - \;{2^{x\; + \;3}} + \;3\; = \;m\;\] có đúng 2 nghiệm \[x \in \left( {1;3} \right)\;\].
Tìm tập nghiệm S của phương trình: \[{4^{x + 1}} + {4^{x - 1}} = 272\]
Tính tổng T tất cả các nghiệm của phương trình\[{4.9^x} - {13.6^x} + {9.4^x} = 0\]