Đề thi THPT QG - 2021 - mã 101
Cho hàm số \[f\left( x \right) = {e^x} + 2\]. Khẳng định nào dưới đây đúng?
A.\[\smallint f\left( x \right)dx = {e^{x - 2}} + C\]
B. \[\smallint f\left( x \right)dx = {e^x} + 2x + C\]
C. \[\smallint f\left( x \right)dx = {e^x} + C\]
D. \[\smallint f\left( x \right)dx = {e^x} - 2x + C\]
Giải bởi qa.haylamdo.com
Đáp án cần chọn là: B
Cho hàm số \[F(x) = {x^2}\;\] là một nguyên hàm của hàm số \[f(x){e^{4x}}\], hàm số f(x) có đạo hàm f′(x). Họ nguyên hàm của hàm số \[f\prime \left( x \right){e^{4x}}\] là
Tìm họ nguyên hàm của hàm số \[f\left( x \right) = \frac{{{x^2} - 2x + 1}}{{x - 2}}\]
Họ nguyên hàm của hàm số \[y = \frac{{2x + 3}}{{2{x^2} - x - 1}}\] là:
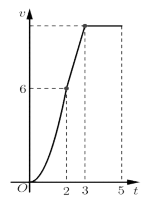
Một chiếc xe đua F1 đạt tới vận tốc lớn nhất là 360km/h. Đồ thị bên biểu thị vận tốc v của xe trong 5 giây đầu tiên kể từ lúc xuất phát. Đồ thị trong 2 giây đầu là một phần của một parabol định tại gốc tọa độ O, giây tiếp theo là đoạn thẳng và sau đúng ba giây thì xe đạt vận tốc lớn nhất. Biết rằng mỗi đơn vị trục hoành biểu thị 1 giây, mỗi đơn vị trực tung biểu thị 10 m/s và trong 5 giây đầu xe chuyển động theo đường thẳng. Hỏi trong 5 giây đó xe đã đi được quãng đường là bao nhiêu?
Cho hàm số f(x) liên tục trên \(\mathbb{R}\) thỏa mãn các điều kiện: f\[\left( 0 \right) = 2\sqrt 2 ,\;f(x) > 0,\forall x \in \mathbb{R}\;\] và \[f(x).f\prime (x) = (2x + 1)\sqrt {1 + {f^2}(x)} ,\forall x \in \mathbb{R}\]. Khi đó giá trị f(1) bằng
Đề thi THPT QG - 2021 - mã 101
Cho hàm số \[f\left( x \right) = {x^2} + 4\]. Khẳng định nào dưới đây đúng?
Hàm số \[y = sinx\;\] là một nguyên hàm của hàm số nào trong các hàm số sau?
\[{\left( {\sin x} \right)^\prime } = \cos x \Rightarrow y = \sin x\] là một nguyên hàm của hàm số\[y = \cos x\]
Cho hàm số \[f\left( x \right) = {e^{ - 2018x + 2017}}\]. Gọi F(x) là một nguyên hàm của f(x) mà \[F\left( 1 \right) = e\]. Chọn mệnh đề đúng:
