Cho ∆ ABC nhọn, đường cao AH. Kẻ HE ⊥ AB (E ∈ AB), HF ⊥ AC (F ∈ AC).
a) Chứng minh: ∆AEH ∽ ∆AHB. Từ đó suy ra AH2 = AE.AB.
b) Chứng minh AE. AB = AF.AC.
c) Cho chu vi các ∆AEF và ∆ACB lần lượt là 20 cm và 30 cm. Tính diện tích ∆AEF và ∆ACB biết diện tích ∆ACB lớn hơn diện tích ∆AEF là 25 cm2.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
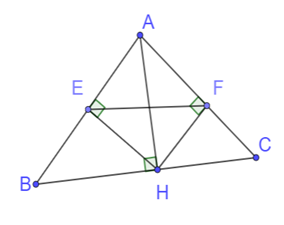
a) Vì AH là đường cao (giả thiết)
Þ AH ⊥ BC
Þ ∆AHB vuông tại H
Lại có HE ⊥ AB (giả thiết)
Þ ∆AEH vuông tại E
Do đó = = 90°
Xét ∆AEH và ∆AHB có:
= (chứng minh trên),
chung
Do đó ∆AEH ∽ ∆ AHB (g.g)
Þ = (tỉ số đồng dạng)
Þ AH2 = AE.AB. (1)
b) Vì AH ⊥ BC (chứng minh câu a)
Þ = 90°
Vì HF ⊥ AC (giả thiết)
Þ = 90°
Xét ∆AFH và ∆AHC có
= = 90°,
chung
Do đó ∆AFH ᔕ ∆AHC (g.g)
Þ = (tỉ số đồng dạng)
Þ AH2 = AF. AC (2)
Từ (1) và (2) suy ra: AE. AB = AF.AC.
c) Theo câu b có: AE. AB = AF.AC
Þ =
Xét ∆AEF và ∆ACB có
chung,
= (chứng minh trên)
Do đó ∆AEF ᔕ ∆ACB (c.g.c)
Þ = = (tỉ số đồng dạng)
Theo tính chất dãy tỉ số bằng nhau ta có:
= = =
(vì chu vi ∆AEF và ∆ACB lần lượt là 20 cm và 30 cm)
Þ = = =
(tính chất tỉ lệ thức)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
(do SABC – SAEF = 25 (cm2))
Þ SAEF = 5.4 = 20 (cm2)
Và SABC = 5.9 = 45 (cm2)
Vậy SAEF = 20 cm2 và SABC = 45 cm2.
Cho x > 1; y > 1 và x + y = 6. Tìm giá trị nhỏ nhất của:
S = 3x + 4y
Giải bài toán bằng cách lập phương trình
Hai ô tô khởi hành một lúc tại A để đi đến B. Ô tô thứ nhất đi với vận tốc 40 km/h. Ô tô thứ hai đi với vận tốc 50 km/h. Biết rằng ô tô thứ nhất tới B chậm hơn ô tô thứ hai 30 phút. Tính độ dài quãng đường AB.
Giải bất phương trình sau và biểu diễn tập nghiệm trên trục số:
− > 2
Cho biết một bể bơi tiêu chuẩn có chiều dài 50 m, chiều rộng 25 m và chiều cao 2,3 m. Người ta bơm nước vào bể sao cho nước cách mép bể 0,5 m. Tính số lít nước đã bơm vào bể.
Cho biểu thức: A = và B = − (x ≠ ±2)
a) Tính giá trị biểu thức A khi x = 3.
b) Rút gọn B.
c) Cho P = . Tìm x để P < 1.
Giải phương trình
a) 5(3x − 2) − 4(5 − 3x) = 1
b) |x + 1| − 2x = 12