A. Hình thang cân
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Phương pháp:
Vẽ hình, sử dụng dấu hiện nhận biết các hình để chọn đáp án đúng.
Cách giải:
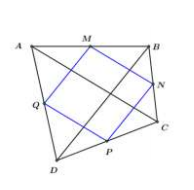
Đáp án C
Giả sử tứ giác ABCD có hai đường chéo AC=BD.
Gọi lần lượt là trung điểm của các cạnh .
Xét ta có:
lần lượt là trung điểm củalà đường trung bình của
Xét ta có:
N, P lần lượt là trung điểm của BC, CD
NP là đường trung bình của
Từ (1) và (2) là hình bình hành (dhnb).
Xét ta có:
M,N lần lượt là trung điểm của AB, BC
MN là đường trung bình của
Mà
là hình thoi. (dhnb).
Tìm điều kiện của tam giác ABC để tứ giác ADGI là hình vuông.
Cho tam giác ABC có AD là phân giác của góc . Từ kẻ các đường thẳng song song với AB và AC, chúng cắt AC,AB tại E và F.
Gọi I là điểm đối xứng của D qua F, tia IA cắt tia DE tại K. Gọi O là giao điểm của AD và EF. Chứng minh G đối xứng với K qua O.
Hình vuông có độ dài đường chéo là 6cm. Độ dài cạnh hình vuông đó là:
Một hình chữ nhật có diện tích . Nếu tăng chiều dài lên hai lần, chiều rộng lên ba lần thì diện tích của hình chữ nhật mới là:
Chứng minh rằng giá trị biểu thức sau không phụ thuộc vào giá trị của biến:
Cho tam giác ABC có AD là phân giác của góc . Từ kẻ các đường thẳng song song với AB và AC, chúng cắt AC, AB tại E và F.
Trên tia AB lấy điểm G sao cho F là trung điểm của AG. Chứng minh tứ giác EFGD là hình bình hành.
Cho tam giác ABC có AD là phân giác của góc . Từ D kẻ các đường thẳng song song với AB và AC, chúng cắt AC,AB tại E và E.
Chứng minh: Tứ giác AEDF là hình thoi.