Cho hình vuông ABCD, M là trung điểm của AB. Gọi P là điểm đối xứng với M qua B, N là điểm đối xứng với C qua B.
Chứng minh N đối xứng với D qua M.
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
Phương pháp:
Chứng minh bằng nhau và thẳng hàng.
Cách giải:
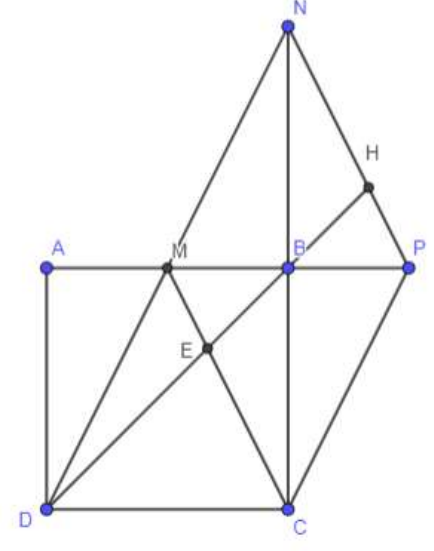
Vì M là trung điểm của AB nên AM = MB.
Xét và ta có:
(cmt)
(gt)
(2cgv) .
Mà (MNPC là hình thoi)
Suy ra . (1)
Tứ giác MPCD có suy ra MPCD là hình bình hành, suy ra .
Lại có thẳng hàng. (2)
Từ (1) và (2) suy ra N đối xứng với D qua M.
Cho hình vuông ABCD, M là trung điểm của AB. Gọi P là điểm đối xứng với M qua B, N là điểm đối xứng với C qua B.
Chứng minh tứ giác MNPC là hình thoi.
Cho các số thực a, b, c thỏa mãn: và .
Tính giá trị của biểu thức .
Cho hình vuông ABCD, M là trung điểm của AB. Gọi P là điểm đối xứng với M qua B, N là điểm đối xứng với C qua B.
Gọi H là giao điểm của DB và NP. Tính tỉ số