Cho vuông tại kẻ tia và điểm khác phía so với đường thẳng BC) Lấy trên tia điểm D sao cho . Chứng minh
 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
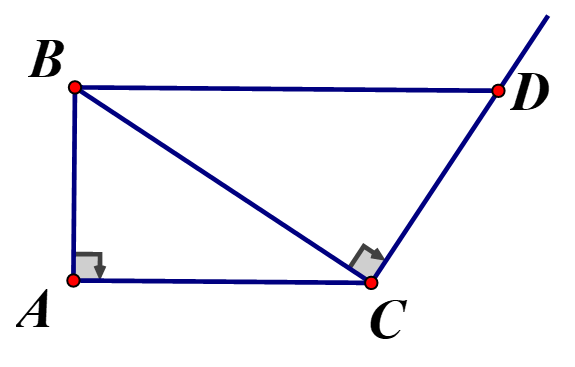
Xét và có:
mà hai góc ở vị trí so le trong
Trong các phương trình sau phương trình nào là phương trình bậc nhất một ẩn