a) Tính tỉ số EMEN
b) Tính độ dài EM,EN
c) Vẽ MK⊥NP(K∈NP) . Chứng minh ΔKMP~ΔMNP
d) Chứng minh MK2=KN.KP
Giải bởi qa.haylamdo.com
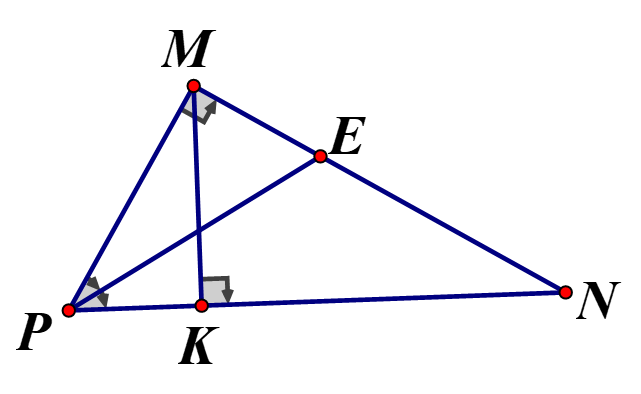
a) Vì PE là đường phân giác ΔMPN⇒MEEN=MPPN=1620=45
b)MEEN=45⇒MEME+EN=44+5⇒MEMN=49⇒ME=4.129=163(cm)⇒EN=203(cm)
c)Xét ΔKMP và ΔMNP có ∠K=∠M=900;∠P chung
⇒ΔKMP~ΔMNP(g-g)
d) Xét ΔMNK và ΔPMKcó ^K1=∠K2=900,∠P=∠KMN (cùng phụ ∠PMK)
⇒ΔMNK~ΔPMK(g−g)⇒MKNK=PKMK⇒MK2=PK.NK
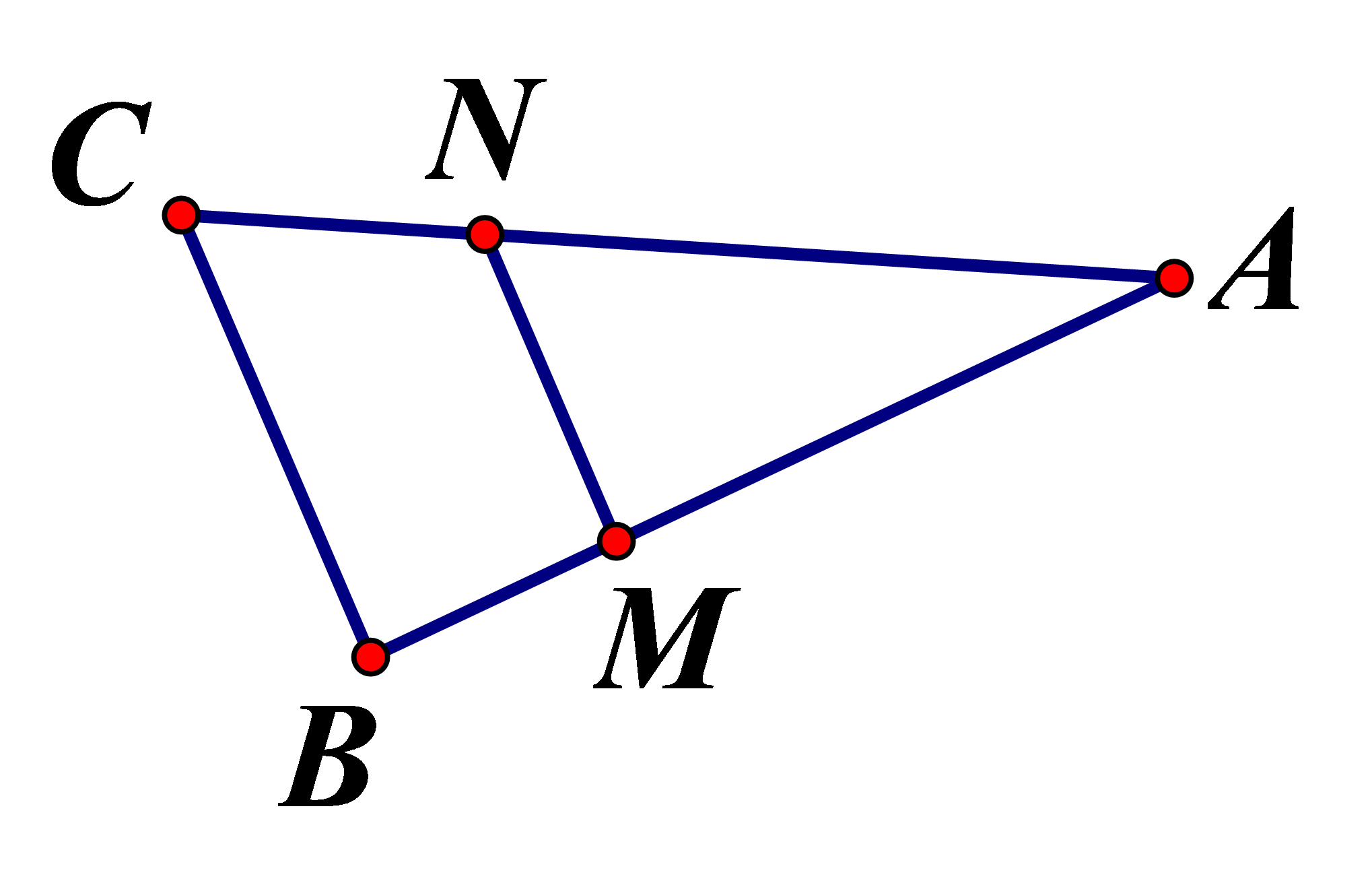
Theo hình vẽ, ta tính được y bằng:
