 Giải bởi qa.haylamdo.com
Giải bởi qa.haylamdo.com
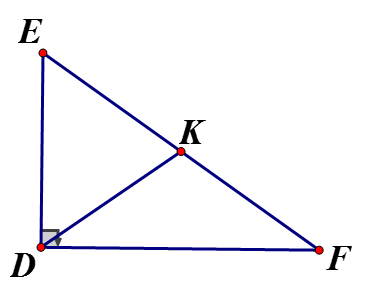
a) Áp dụng định lý Pytago vào ΔDEF vuông tại D ⇒EF2=DE2+DF2
Hay EF2=32+42=25⇒EF=√25=5(cm)
b) ΔDEF vuông tại D, có DK là đường trung tuyến ⇒DK=12EF=12.5=2,5(cm)
Đoạn thẳng MN là ………………………………………........
Cho CD=8cm,EF=14cm. Độ dài của MN bằng